
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 281 Атанасян — Подробные Ответы
Что представляет собой множество всех точек плоскости, равноудалённых от двух данных параллельных прямых?
Множество всех точек плоскости, равноудалённых от двух данных параллельных прямых, представляет собой прямую, которая проходит параллельно этим прямым и находится на равном расстоянии от них.
Дано: две параллельные прямые a и b. Требуется найти множество всех точек, равноудаленных от этих прямых.
Решение:
1. Рассмотрим расстояние между двумя параллельными прямыми a и b. Это расстояние является постоянным, так как прямые параллельны.
2. Точка, равноудаленная от двух параллельных прямых, должна находиться на одинаковом расстоянии от каждой из них. Для этого нужно провести прямую, которая будет параллельна данным прямым a и b и находиться посередине между ними.
3. Чтобы построить такую прямую, можно воспользоваться следующим методом:
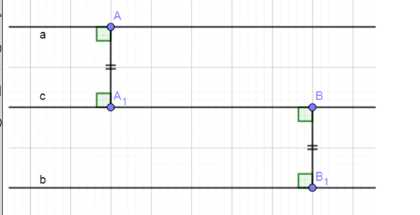
— Проведем перпендикуляры из произвольных точек на прямой a и прямой b.
— Найдем середины этих перпендикуляров. Все такие середины будут лежать на искомой прямой.
4. Искомая прямая будет параллельна прямым a и b, так как она проходит через середины отрезков, соединяющих точки на прямых a и b, а эти отрезки перпендикулярны данным прямым.
5. Таким образом, множество всех точек, равноудаленных от двух параллельных прямых a и b, является прямой, которая проходит параллельно этим прямым и находится на равном расстоянии от них.
Вывод: искомое множество точек – это прямая, расположенная посередине между параллельными прямыми a и b.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!