ГДЗ по Геометрии 7 класс Номер 265 Атанасян — Подробные Ответы

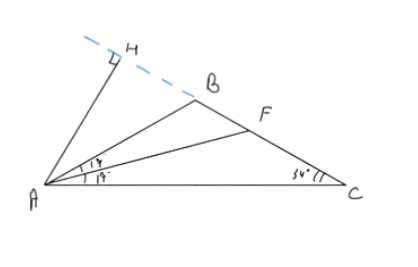
В равнобедренном треугольнике ABC с основанием АС проведены биссектриса AF и высота АН. Найдите углы треугольника AHF, если ∠B = 112°.

ΔABC равнобедренный, AB = BC, ∠B = 112°.

1. Углы при основании равны: ∠A = ∠C = (180° — ∠B) / 2 = (180° — 112°) / 2 = 68° / 2 = 34°.
2. AF — биссектриса угла ∠A, значит ∠BAF = ∠CAF = ∠A / 2 = 34° / 2 = 17°.
3. В треугольнике AHF:
∠HFA = 180° — (∠B + ∠BAF) = 180° — (112° + 17°) = 51°.
4. ∠HAF = 90° — ∠HFA = 90° — 51° = 39°.

Ответ: ∠HAF = 39°, ∠HFA = 51°.

Дано:
Треугольник ABC равнобедренный с основанием AC. Угол при вершине B равен 112°. Проведены биссектриса AF и высота AH. Требуется найти углы треугольника AHF.

Решение:

1. Так как треугольник ABC равнобедренный с основанием AC, углы при основании равны. Найдем их:
Угол при вершине B равен 112°, а сумма углов треугольника равна 180°. Следовательно, углы при основании вычисляются как:
∠A = ∠C = (180° — ∠B) / 2 = (180° — 112°) / 2 = 68° / 2 = 34°.

2. AF — это биссектриса угла ∠A. Она делит угол ∠A на два равных угла. Найдем каждый из них:
∠BAF = ∠CAF = ∠A / 2 = 34° / 2 = 17°.

3. Рассмотрим треугольник AHF. В нем:
— Угол ∠HFA — внешний угол по отношению к треугольнику BAF. Найдем его:
∠HFA = 180° — (∠B + ∠BAF) = 180° — (112° + 17°) = 180° — 129° = 51°.

4. Угол ∠HAF в треугольнике AHF можно найти, так как AH является высотой, а значит, угол ∠HAF дополняет угол ∠HFA до 90° (по свойству прямоугольного треугольника):
∠HAF = 90° — ∠HFA = 90° — 51° = 39°.

Ответ: угол HAF равен 39°, угол HFA равен 51°.