
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 239 Атанасян — Подробные Ответы
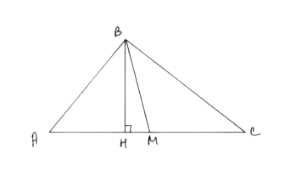
Докажите, что в треугольнике медиана не меньше высоты, проведённой из той же вершины.
1. Рассмотрим треугольник BDK, где BK — высота, а BD — медиана. Угол BDK равен 90°, поэтому гипотенуза BD всегда больше катета BK (свойство прямоугольного треугольника). Следовательно, BD ≥ BK.
2. Если треугольник ABC равнобедренный или равносторонний, то медиана BD и высота BK совпадают, и BD = BK.
Таким образом, медиана всегда не меньше высоты.
Рассмотрим треугольник ABC. Пусть BD – медиана, проведенная из вершины B, а BK – высота, проведенная из той же вершины B.
1. Точка D – середина стороны AC. Это свойство медианы, так как медиана делит противоположную сторону пополам.
2. Высота BK опущена перпендикулярно на сторону AC, то есть угол BKA равен 90 градусам.
3. Рассмотрим треугольник BDK. В этом треугольнике:
— BK – катет,
— BD – гипотенуза,
— угол BDK равен 90 градусам.
4. В прямоугольном треугольнике гипотенуза всегда больше любого из катетов. Следовательно, BD больше или равно BK.
5. Если треугольник ABC равнобедренный с основанием AC, то медиана BD и высота BK совпадают, и в этом случае BD равно BK.
6. Если треугольник ABC равносторонний, то медиана BD и высота BK также совпадают, и в этом случае BD равно BK.
7. В общем случае медиана BD всегда больше или равна высоте BK, что следует из геометрических свойств медиан и высот в треугольниках.
Таким образом, доказано, что медиана, проведенная из вершины, всегда не меньше высоты, проведенной из той же вершины.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!