
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7-9 класс Номер 2 Атанасян — Подробные Ответы
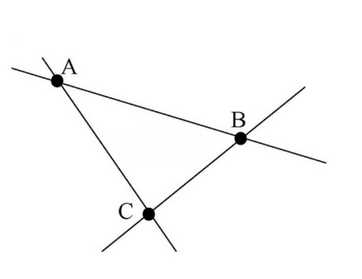
Отметьте три точки А, В и С, не лежащие на одной прямой, и проведите прямые АВ, ВС и СА.
Точки А, В и С расположены так, чтобы не лежать на одной прямой. Проведены прямые АВ, ВС и СА, соединяющие эти точки. А, В и С — точки, не лежащие на одной прямой. Линии АВ, ВС и СА соединяют эти точки, образуя треугольник.
1. Точки А, В и С расположены так, чтобы не лежать на одной прямой. Это значит, что никакие две точки не совпадают, и при этом они не находятся на одной линии. Если бы они лежали на одной прямой, то углы, образованные этими точками, были бы равны 0° или 180°, а это противоречит условию задачи.
2. Проведены прямые АВ, ВС и СА, соединяющие эти точки. Прямая АВ — это линия, проходящая через точки А и В, прямая ВС — через В и С, прямая СА — через С и А. Эти линии соединяют указанные точки, образуя замкнутую фигуру.
А, В и С — точки, не лежащие на одной прямой, то есть они образуют треугольник. Треугольник — это фигура, образованная тремя отрезками, соединяющими три точки, не лежащие на одной прямой. Линии АВ, ВС и СА соединяют эти точки, образуя треугольник с углами, сумма которых равна \(180^\circ\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!