
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 191 Атанасян — Подробные Ответы
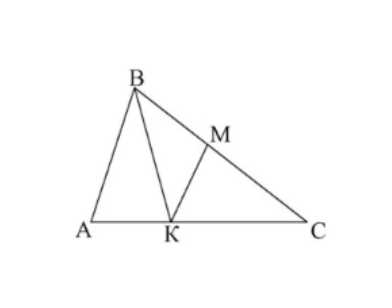
Отрезок ВK — биссектриса треугольника ABC. Через точку K проведена прямая, пересекающая сторону ВС в точке М так, что ВМ = МK. Докажите, что прямые KМ и AB параллельны.
Треугольник BMK равнобедренный, так как BM = MK. Углы при основании равны, то есть угол MBK равен углу MKB. Так как BK является биссектрисой угла B, то угол ABK равен углу CBK. Углы ABK и MKB накрест лежащие, поэтому они равны. Следовательно, AB параллельна MK.
Рассмотрим треугольник ABC, в котором проведена биссектриса BK и точка M является серединой отрезка BC, то есть BM = MK.
1. Так как BM = MK, то треугольник BMK является равнобедренным. По свойству равнобедренного треугольника углы при основании равны, то есть угол MBK равен углу MKB.
2. BK является биссектрисой угла B, следовательно, угол ABK равен углу CBK.
3. Рассмотрим углы ABK и MKB. Угол ABK образован прямой AB и биссектрисой BK, а угол MKB образован прямой MK и биссектрисой BK. Эти углы являются накрест лежащими при пересечении прямых AB и MK секущей BK.
4. Так как угол ABK равен углу CBK, а угол CBK равен углу MKB (по равенству углов при основании равнобедренного треугольника BMK), то угол ABK равен углу MKB.
5. Из равенства накрест лежащих углов следует, что прямые AB и MK параллельны.
Таким образом, доказано, что AB параллельна MK.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!