
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 18 Атанасян — Подробные Ответы
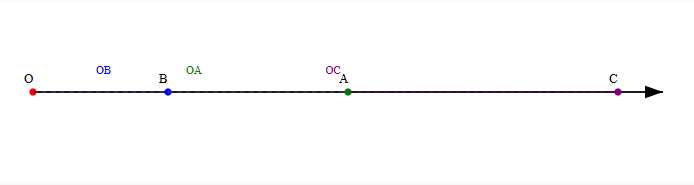
На луче с началом О отмечены точки А, В и С так, что точка В лежит между точками О и А, а точка А — между точками О и С. Сравните отрезки ОВ и ОА, ОС и ОА, ОВ и ОС.
Точка В лежит между О и А, значит \(OV < OA\). Точка А лежит между О и С, значит \(OA < OC\). Из этого следует, что \(OV < OA < OC\). Итоговые сравнения:
\(OV < OA\),
\(OA < OC\),
\(OV < OC\).
1 Луч:
Начало луча находится в точке О, направлен вправо. Это значит, что все точки расположены на одном направлении от точки О.
3 Расположение точек:
Точка В расположена между точками О и А, значит \(OV < OA\).
Точка А расположена между точками О и С, значит \(OA < OC\).
Все точки находятся на одном луче, следовательно, порядок по длине отрезков сохраняется. 7 Отрезки:
Отрезок \(OV\) короче отрезка \(OA\), так как точка В лежит между О и А, значит \(OV < OA\).
Отрезок \(OA\) короче отрезка \(OC\), так как точка А лежит между О и С, значит \(OA < OC\).
Отрезок \(OV\) короче отрезка \(OC\), так как \(OV < OA\) и \(OA < OC\), значит \(OV < OC\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!