ГДЗ по Геометрии 7-9 класс Номер 15 Атанасян — Подробные Ответы

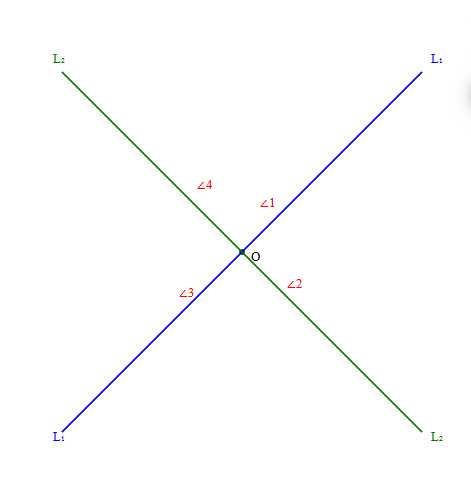
Сколько неразвёрнутых углов образуется при пересечении двух прямых?

При пересечении двух прямых образуются четыре угла. Все они являются неразвёрнутыми, так как каждый угол меньше 180°.

Обозначим углы при пересечении как \(\angle 1, \angle 2, \angle 3, \angle 4\). Прямые делят плоскость на четыре части, каждая из которых соответствует одному углу.

Ответ: при пересечении двух прямых образуется 4 неразвёрнутых угла.

1. При пересечении двух прямых образуются четыре угла. Эти углы расположены вокруг точки пересечения и образуют полный круг в 360°.

2. Каждый из углов является неразвёрнутым, так как величина каждого угла меньше 180°. Неразвёрнутый угол — это угол, который меньше или равен 180°, но не равен ровно 180°.

3. Обозначим углы при пересечении как \(\angle 1\), \(\angle 2\), \(\angle 3\) и \(\angle 4\). Они расположены по порядку вокруг точки пересечения.

4. Сумма всех четырёх углов равна 360°, то есть \(\angle 1 + \angle 2 + \angle 3 + \angle 4 = 360^\circ\).

5. Противоположные углы при пересечении двух прямых равны, следовательно, \(\angle 1 = \angle 3\) и \(\angle 2 = \angle 4\).

6. Из равенства противоположных углов и суммы всех углов можно вывести, что каждый угол меньше 180°, то есть неразвёрнутый.

7. Таким образом, при пересечении двух прямых образуются именно четыре неразвёрнутых угла.

8. Это объясняется тем, что две прямые делят плоскость на четыре части, каждая из которых соответствует одному углу.

9. Следовательно, количество неразвёрнутых углов при пересечении двух прямых равно 4.

10. Ответ: 4 угла.