ГДЗ по Геометрии 7-9 класс Номер 14 Атанасян — Подробные Ответы

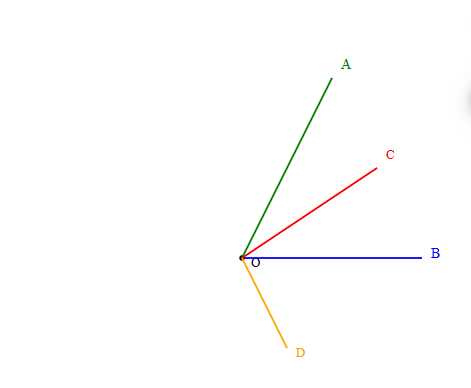
Начертите неразвёрнутый угол АОВ и проведите:
а) луч ОС, который делит угол АОВ на два угла;
б) луч OD, который не делит угол АОС на два угла.

Начертите неразвёрнутый угол АОВ.

а) Луч ОС делит угол АОВ на два угла, значит угол АОС равен углу СОВ.
б) Луч OD не делит угол АОС на два угла, то есть угол АОД равен углу ДОС, но при этом OD лежит внутри угла АОВ, не создавая равных частей для угла АОС.

Таким образом:
— Луч ОС — биссектриса угла АОВ, делит угол на два равных угла.
— Луч OD — не является биссектрисой угла АОС, не делит его на два угла.

1. Начертите неразвёрнутый угол АОВ. Для этого проведите лучи ОА и ОВ, исходящие из точки О, так чтобы угол АОВ был меньше 180°.

2. Постройте луч ОС, который делит угол АОВ на два равных угла. Это означает, что луч ОС является биссектрисой угла АОВ. Тогда выполняется равенство углов:
угол \(АОС = \) угол \(СОВ\).

3. Луч ОС располагается внутри угла АОВ и делит его точно пополам, то есть
\(\angle АОВ = \angle АОС + \angle СОВ\),
и при этом
\(\angle АОС = \angle СОВ\).

4. Теперь проведите луч OD, который не делит угол АОС на два угла. Луч OD должен находиться внутри угла АОВ, но не быть биссектрисой угла АОС.

5. Это значит, что угол АОС не равен сумме двух углов, образованных лучом OD, то есть
\(\angle АОС \neq \angle АОД + \angle ДОС\),
или если и равен, то \(\angle АОД \neq \angle ДОС\).

6. Таким образом, луч OD не делит угол АОС на два равных угла, а просто лежит внутри угла АОВ, не создавая равенства углов при делении угла АОС.

7. Итог:
— Луч ОС — биссектриса угла АОВ, делит его на два равных угла.
— Луч OD — не биссектриса угла АОС, не делит его на два равных угла.