ГДЗ по Геометрии 7 класс Номер 11 Атанасян — Подробные Ответы

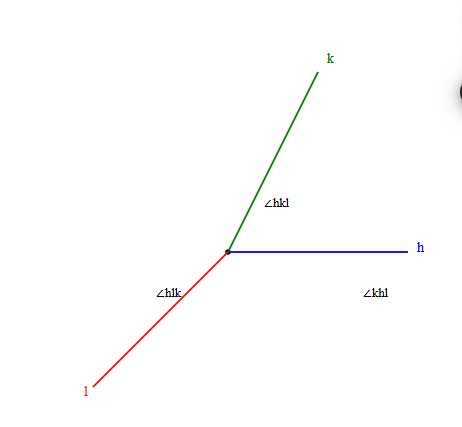
Начертите три луча h, k и l с общим началом. Назовите все углы, образованные данными лучами.

Начертим три луча \(h\), \(k\) и \(l\) с общим началом.

Образованные углы:
— \(\angle hkl\) — угол между лучами \(h\) и \(k\)
— \(\angle khl\) — угол между лучами \(k\) и \(l\)
— \(\angle lhk\) — угол между лучами \(l\) и \(h\)

Все углы имеют общее начало и образованы парами данных лучей.

1. Начертим три луча \(h\), \(k\) и \(l\), исходящих из одной точки, которую обозначим \(O\). Эти лучи имеют общее начало \(O\).

2. Рассмотрим пары лучей, чтобы определить углы, образованные ими. Угол — это часть плоскости, ограниченная двумя лучами с общим началом.

3. Угол между лучами \(h\) и \(k\) обозначим как \(\angle hkl\). Он образован лучами \(h\) и \(k\) с началом в точке \(O\).

4. Угол между лучами \(k\) и \(l\) обозначим как \(\angle khl\). Он образован лучами \(k\) и \(l\) с общим началом в точке \(O\).

5. Угол между лучами \(l\) и \(h\) обозначим как \(\angle lhk\). Он образован лучами \(l\) и \(h\) с общим началом в точке \(O\).

6. Таким образом, три луча образуют три угла: \(\angle hkl\), \(\angle khl\) и \(\angle lhk\).

7. Каждый из этих углов можно измерить в градусах или радианах, в зависимости от задачи.

8. Важно, что все углы имеют общее начало \(O\), так как все лучи исходят из этой точки.

9. Итог: три луча \(h\), \(k\), \(l\) с общим началом образуют три угла — \(\angle hkl\), \(\angle khl\), \(\angle lhk\).

10. Это соответствует рисунку и условию задачи, где все углы названы правильно и полно.