ГДЗ по Геометрии 7-9 класс Номер 1 Атанасян

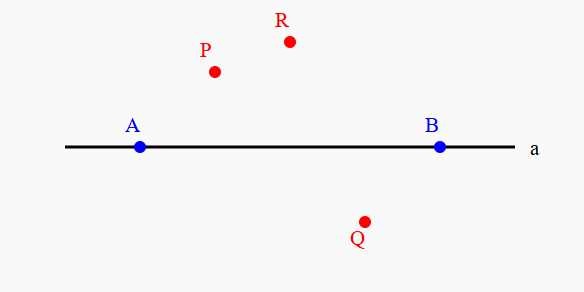
Проведите прямую, обозначьте её буквой a и отметьте точки A и B, лежащие на этой прямой, и точки P, Q и R, не лежащие на ней. Опишите взаимное расположение точек A, B, P, Q, R и прямой a, используя символы ∈ и ∉.

Пусть прямая \( а \) содержит точки \( A \) и \( B \), тогда \( A \in а \), \( B \in а \).

Точки \( P \), \( Q \) и \( R \) не лежат на прямой \( а \), значит \( P \notin а \), \( Q \notin а \), \( R \notin а \).

1. Проведём прямую и обозначим её буквой \( а \).

2. Отметим на прямой две точки \( A \) и \( B \). По определению, эти точки лежат на прямой \( а \), значит \( A \in а \) и \( B \in а \).

3. Теперь отметим точки \( P \), \( Q \) и \( R \), которые не лежат на прямой \( а \). Это значит, что \( P \notin а \), \( Q \notin а \) и \( R \notin а \).

4. Рассмотрим взаимное расположение точек \( A \) и \( B \) на прямой \( а \). Точки \( A \) и \( B \) лежат на одной прямой, поэтому можно записать \( A \in а \) и \( B \in а \).

5. Точки \( P \), \( Q \), \( R \) расположены вне прямой \( а \), то есть \( P \notin а \), \( Q \notin а \), \( R \notin а \).

6. Используя символы принадлежности и непринадлежности, запишем: \( A \in а \), \( B \in а \), \( P \notin а \), \( Q \notin а \), \( R \notin а \).

7. Таким образом, прямая \( а \) содержит только точки \( A \) и \( B \), а точки \( P \), \( Q \) и \( R \) находятся вне этой прямой.

8. Если рассматривать точки \( P \), \( Q \), \( R \) относительно прямой \( а \), то они не пересекаются с ней, так как не лежат на ней.

9. Итоговое взаимное расположение: \( A \in а \), \( B \in а \), \( P \notin а \), \( Q \notin а \), \( R \notin а \).

10. Таким образом, задача решена согласно условию и рисунку.