ГДЗ по Геометрии 11 класс Задание 8 Номер 8 Атанасян — Подробные Ответы

Высота конуса равна 4, а диаметр основания равен 6. Образующая конуса равна \(5\).

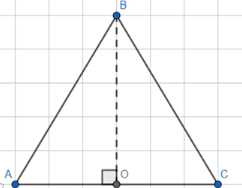
Дано: \(BO \perp AC\), \(AC = 6\), \(BO = 4\). Треугольник \(ABC\) равнобедренный (\(AB = BC\)).

1. Так как \(\triangle ABC\) равнобедренный и \(BO\) — высота к основанию \(AC\), то \(BO\) также медиана:
\(AO = OC = \frac{AC}{2} = \frac{6}{2} = 3\).

2. В прямоугольном \(\triangle AOB\) (\( \angle O = 90^\circ \)):
\(AB^2 = AO^2 + BO^2 = 3^2 + 4^2 = 9 + 16 = 25\),
откуда \(AB = \sqrt{25} = 5\).

Ответ: \(5\).

Дано: треугольник \( ABC \) является равнобедренным, где \( BO \) перпендикулярен \( AC \), \( AC = 6 \) и \( BO = 4 \).

Решение:
1. Так как треугольник \( ABC \) является равнобедренным, то \( AB = BC \).
2. Поскольку \( BO \) перпендикулярен \( AC \), то \( BO \) является высотой треугольника \( ABC \). Согласно свойству равнобедренного треугольника, высота \( BO \) также является медианой.
3. Чтобы найти длину \( AB \), воспользуемся тем, что \( BO \) является медианой. Тогда \( AO = OC = \frac{AC}{2} = \frac{6}{2} = 3 \).
4. В прямоугольном треугольнике \( AOB \) (\( \angle O = 90^\circ \)), применим теорему Пифагора:
\( AB^2 = AO^2 + BO^2 = 3^2 + 4^2 = 9 + 16 = 25 \)
5. Следовательно, \( AB = \sqrt{25} = 5 \).

Ответ: \( 5 \).