
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Задание 8 Номер 7 Атанасян — Подробные Ответы
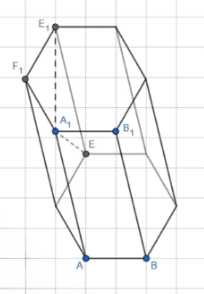
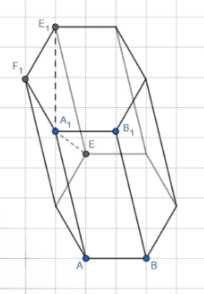
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, где все рёбра равны 49, угол E1EA1 равен \(60^\circ\).
На рисунке изображена правильная призма, в которой AB = AA₁ = 49.
Найдем угол E₁EA₁.
1) Рассмотрим треугольник E₁F₁A₁:
E₁F₁ = F₁A₁ = AB = 49, ∠F₁ = 120°
По теореме косинусов:
E₁A₁² = E₁F₁² + F₁A₁² — 2·E₁F₁·F₁A₁·cos F₁
E₁A₁² = 49² + 49² — 2·49·49·cos 120°
E₁A₁² = 49² + 49² — 2·49·49·(-0,5)
E₁A₁² = 49² + 49² + 49²
E₁A₁² = 3·49²
E₁A₁ = √(3·49²) = 49·√3
2) В прямоугольном треугольнике E₁A₁E:
tg E = E₁A₁/EE₁ = √3
Так как tg E = √3, то ∠E = 60°
Ответ: 60°.
Рассмотрим задачу о нахождении угла E₁EA₁ в правильной шестиугольной призме.
Дано:
— правильная призма;
— AB = AA₁ = 49;
Требуется найти: ∠E₁EA₁.
Решение:
Для начала проанализируем геометрическую конфигурацию. На рисунке изображена правильная призма, где точки A, B, F находятся в нижнем основании, а точки A₁, B₁, F₁ — в верхнем основании. Точка E является центром нижнего основания, а E₁ — центром верхнего основания.
Нам нужно найти угол между прямыми EE₁ и EA₁, то есть ∠E₁EA₁.
Шаг 1: Найдем длину отрезка E₁A₁.
Для этого рассмотрим треугольник E₁F₁A₁ в верхнем основании призмы.
Поскольку призма правильная, то E₁F₁ = F₁A₁ = AB = 49.
Угол F₁ в этом треугольнике равен 120°, так как в правильном шестиугольнике центральный угол равен 60°, а угол между соседними радиусами составляет 60°. Следовательно, угол между радиусами, идущими к несоседним вершинам, равен 120°.
Применим теорему косинусов для треугольника E₁F₁A₁:
(E₁A₁)² = (E₁F₁)² + (F₁A₁)² — 2·(E₁F₁)·(F₁A₁)·cos(∠F₁)
(E₁A₁)² = 49² + 49² — 2·49·49·cos(120°)
Учитывая, что cos(120°) = -0,5, получаем:
(E₁A₁)² = 49² + 49² — 2·49·49·(-0,5)
(E₁A₁)² = 49² + 49² + 49²
(E₁A₁)² = 3·49²
(E₁A₁) = 49·√3
Шаг 2: Рассмотрим треугольник E₁A₁E.
Этот треугольник является прямоугольным, так как EE₁ перпендикулярна основанию призмы.
В этом треугольнике:
— EE₁ = AA₁ = 49 (высота призмы)
— E₁A₁ = 49·√3 (найдено выше)
— ∠E₁EA₁ — искомый угол
В прямоугольном треугольнике E₁A₁E угол E можно найти через тангенс:
tg(∠E) = E₁A₁/EE₁ = (49·√3)/49 = √3
Угол, тангенс которого равен √3, составляет 60°.
Таким образом, искомый угол ∠E₁EA₁ = 60°.
Ответ: 60°.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!