ГДЗ по Геометрии 11 класс Задание 8 Номер 6 Атанасян — Подробные Ответы

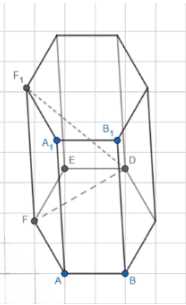
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, где все рёбра равны 23, расстояние между точками D и F1 равно \(23\sqrt{3}\).

Рассмотрим задачу о нахождении длины отрезка DF₁ в правильной призме.

Дано:
— правильная призма ABCDEFA₁B₁C₁D₁E₁F₁
— AB = AA₁ = 23

Решение:

Сначала найдем длину отрезка FD. Для этого рассмотрим треугольник FED.
В этом треугольнике:
— FE = ED = AB = 23 (так как в правильной призме все ребра основания равны)
— угол E = 120° (так как основание — правильный шестиугольник)

Применим теорему косинусов для треугольника FED:
\(FD^2 = FE^2 + ED^2 — 2 \cdot FE \cdot ED \cdot \cos E\)

Подставим известные значения:
\(FD^2 = 23^2 + 23^2 — 2 \cdot 23^2 \cdot \cos 120°\)

Так как \(\cos 120° = -0,5\), получаем:
\(FD^2 = 23^2 + 23^2 — 2 \cdot 23^2 \cdot (-0,5) = 23^2 + 23^2 + 23^2 = 3 \cdot 23^2\)

Теперь рассмотрим прямоугольный треугольник DF₁F:
— DF — найденная нами сторона
— FF₁ = AA₁ = 23 (высота призмы)
— DF₁ — искомая диагональ

По теореме Пифагора:
\(DF_1^2 = FD^2 + FF_1^2 = 3 \cdot 23^2 + 23^2 = 4 \cdot 23^2\)

Отсюда:
\(DF_1 = \sqrt{4 \cdot 23^2} = 2 \cdot 23 = 46\)

Ответ: 46.

Рассмотрим задачу о нахождении длины отрезка DF₁ в правильной призме.

Дано: правильная призма ABCDEFA₁B₁C₁D₁E₁F₁, AB = AA₁ = 23.
Найти: DF₁.

Решение:

Начнем с анализа геометрической фигуры. У нас имеется правильная призма, в основании которой лежит правильный шестиугольник ABCDEF. Верхнее основание призмы — правильный шестиугольник A₁B₁C₁D₁E₁F₁. Высота призмы равна AA₁ = 23.

Для нахождения длины отрезка DF₁ разобьем решение на логические этапы.

Этап 1: Найдем длину отрезка FD.
Для этого рассмотрим треугольник FED в нижнем основании призмы. Так как основание — правильный шестиугольник, то все его стороны равны между собой, то есть FE = ED = AB = 23.

Также в правильном шестиугольнике углы между соседними сторонами равны 120°. Поэтому угол E в треугольнике FED равен 120°.

Применим теорему косинусов для треугольника FED:
\(FD^2 = FE^2 + ED^2 — 2 \cdot FE \cdot ED \cdot \cos E\)

Подставим известные значения:
\(FD^2 = 23^2 + 23^2 — 2 \cdot 23 \cdot 23 \cdot \cos 120°\)

Вычислим значение косинуса:
\(\cos 120° = -0,5\)

Продолжим вычисления:
\(FD^2 = 23^2 + 23^2 — 2 \cdot 23^2 \cdot (-0,5)\)
\(FD^2 = 529 + 529 — 2 \cdot 529 \cdot (-0,5)\)
\(FD^2 = 1058 + 529 = 1587\)

Можно также записать это в виде:
\(FD^2 = 23^2 + 23^2 + 23^2 = 3 \cdot 23^2\)

Таким образом, \(FD^2 = 3 \cdot 23^2\).

Этап 2: Найдем длину отрезка DF₁.
Рассмотрим треугольник DF₁F. Этот треугольник является прямоугольным, так как отрезок FF₁ перпендикулярен плоскости нижнего основания призмы.

В этом треугольнике:
— DF — сторона, длину которой мы нашли на предыдущем этапе
— FF₁ = AA₁ = 23 (высота призмы)
— DF₁ — искомая диагональ

По теореме Пифагора:
\(DF_1^2 = DF^2 + FF_1^2\)

Подставим известные значения:
\(DF_1^2 = 3 \cdot 23^2 + 23^2 = 4 \cdot 23^2\)

Извлечем квадратный корень:
\(DF_1 = \sqrt{4 \cdot 23^2} = 2 \cdot 23 = 46\)

Проверка: \(46^2 = 2116\), а \(4 \cdot 23^2 = 4 \cdot 529 = 2116\). Значит, наши вычисления верны.

Таким образом, длина отрезка DF₁ равна 46 единиц.

Ответ: 46.