ГДЗ по Геометрии 11 класс Задание 8 Номер 5 Атанасян — Подробные Ответы

Диагональ основания правильной четырёхугольной пирамиды равна 6, а высота пирамиды равна 4. Длина бокового ребра равна \(5\).

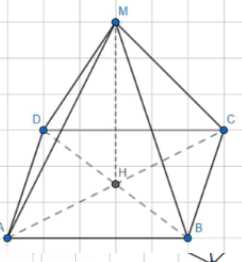
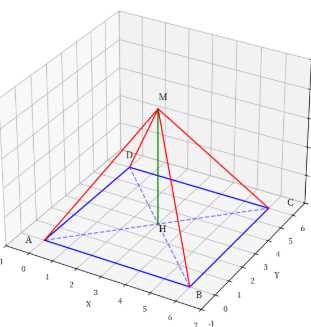
Рассмотрим задачу с пирамидой MABCD, где ABCD — квадрат.

Дано:
— ABCD — квадрат
— MH — высота пирамиды, MH = 4
— AC = 6
— H — точка пересечения диагоналей квадрата

Найдем длину AH:
Поскольку H — точка пересечения диагоналей квадрата, то AH = CH = \(\frac{1}{2} \cdot AC = \frac{1}{2} \cdot 6 = 3\)

Теперь рассмотрим прямоугольный треугольник AHM:
— AH = 3
— MH = 4
— Угол AHM = 90° (так как MH перпендикулярна плоскости ABCD)

По теореме Пифагора:
\(AM^2 = AH^2 + MH^2 = 3^2 + 4^2 = 9 + 16 = 25\)
\(AM = \sqrt{25} = 5\)

Ответ: 5.

Рассмотрим задачу о нахождении длины отрезка AM в пирамиде MABCD.

Дано:
— ABCD — квадрат
— M — вершина пирамиды
— MH — высота пирамиды, перпендикулярная плоскости ABCD
— AC = 6
— MH = 4
— Требуется найти AM

Решение:

1) Сначала разберемся с геометрией задачи. У нас есть пирамида MABCD, в основании которой лежит квадрат ABCD. Точка M — вершина пирамиды, а MH — высота пирамиды, где H — точка в плоскости основания.

2) Из условия известно, что MH перпендикулярна плоскости ABCD, то есть MH ⊥ ABCD. Также указано, что H принадлежит пересечению диагоналей квадрата, то есть H = AC ∩ BD.

3) Найдем координаты точки H. Поскольку H — точка пересечения диагоналей квадрата ABCD, то H является центром квадрата. В квадрате диагонали пересекаются и делятся точкой пересечения пополам. Поэтому:

AH = CH = \(\frac{1}{2} \cdot AC = \frac{1}{2} \cdot 6 = 3\)

4) Теперь рассмотрим прямоугольный треугольник AHM:
— Угол AHM = 90°, так как MH перпендикулярна плоскости ABCD, а значит и любой прямой в этой плоскости, проходящей через H, в том числе и AH.
— Катет AH = 3 (мы только что вычислили)
— Катет MH = 4 (дано по условию)

5) Применим теорему Пифагора для нахождения гипотенузы AM в прямоугольном треугольнике AHM:

\(AM^2 = AH^2 + MH^2\)

\(AM^2 = 3^2 + 4^2\)

\(AM^2 = 9 + 16\)

\(AM^2 = 25\)

\(AM = \sqrt{25} = 5\)

6) Проверим результат. Мы получили, что AM = 5. Это соответствует условию задачи и согласуется с геометрическим смыслом: длина ребра пирамиды от вершины M до вершины основания A равна 5 единицам.

Важно отметить, что в данной задаче мы использовали свойства квадрата:
— Диагонали квадрата пересекаются и делятся точкой пересечения пополам
— Диагонали квадрата равны между собой
— Диагонали квадрата взаимно перпендикулярны

Также мы использовали свойство высоты пирамиды: высота перпендикулярна плоскости основания.

Таким образом, мы нашли длину ребра AM пирамиды MABCD, которая равна 5 единицам.

Ответ: 5.