ГДЗ по Геометрии 11 класс Задание 8 Номер 4 Атанасян — Подробные Ответы

В правильной треугольной пирамиде SABC, где медианы основания пересекаются в точке M, объём пирамиды равен 1, а площадь треугольника ABC, если MS=1, равна \(\frac{1}{3}\).

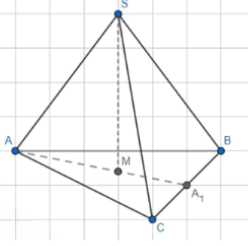
В правильном треугольнике ABC медианы AA₁ и BB₁ пересекаются в точке M, которая является центром треугольника.

В пирамиде SABC точка M лежит в основании, а высота SM перпендикулярна плоскости основания ABC.

Объем пирамиды вычисляется по формуле \(V = \frac{1}{3} \cdot S_{осн} \cdot h\), где \(S_{осн}\) — площадь основания, а \(h\) — высота пирамиды.

Нам дано, что \(V = 1\) и \(MS = 1\), то есть высота пирамиды \(h = MS = 1\).

Подставим в формулу объема: \(V = \frac{1}{3} \cdot S_{ABC} \cdot 1 = \frac{1}{3} \cdot S_{ABC} = 1\)

Отсюда получаем: \(\frac{1}{3} \cdot S_{ABC} = 1\), следовательно \(S_{ABC} = 3\).

Ответ: 3.

Рассмотрим задачу о нахождении площади основания пирамиды SABC.

Дано: правильный треугольник ABC в основании пирамиды SABC; медианы AA₁ и BB₁ в треугольнике ABC; точка M является точкой пересечения медиан AA₁ и BB₁; объем пирамиды V = 1; расстояние от вершины S до точки M равно MS = 1.

Требуется найти: площадь основания пирамиды, то есть площадь треугольника ABC (S₍ₐₑₒ₎).

Решение:

Шаг 1: Проанализируем свойства точки M в треугольнике ABC.
В любом треугольнике медианы пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины. Эта точка называется центроидом или центром масс треугольника. Таким образом, M — это центр масс треугольника ABC. В правильном треугольнике центр масс совпадает с центром описанной окружности, центром вписанной окружности и точкой пересечения высот.

Шаг 2: Рассмотрим геометрическую конфигурацию пирамиды SABC.
Вершина S пирамиды расположена над точкой M таким образом, что SM перпендикулярна плоскости ABC. Это означает, что SM является высотой пирамиды, проведенной к основанию ABC.

Шаг 3: Вычислим объем пирамиды SABC.
Объем пирамиды вычисляется по формуле: \(V = \frac{1}{3} \cdot S_{осн} \cdot h\), где \(S_{осн}\) — площадь основания (в нашем случае площадь треугольника ABC), а \(h\) — высота пирамиды (в нашем случае длина отрезка SM).

Шаг 4: Подставим известные значения в формулу объема.
По условию задачи, объем пирамиды V = 1, а высота пирамиды SM = 1.
Подставим эти значения в формулу объема:
\(V = \frac{1}{3} \cdot S_{ABC} \cdot SM = 1\)
\(\frac{1}{3} \cdot S_{ABC} \cdot 1 = 1\)
\(\frac{1}{3} \cdot S_{ABC} = 1\)

Шаг 5: Найдем площадь основания пирамиды.
Из предыдущего шага получаем:
\(S_{ABC} = 3 \cdot 1 = 3\)

Таким образом, площадь правильного треугольника ABC, являющегося основанием пирамиды SABC, равна 3 квадратным единицам.

Проверка: Подставим найденное значение \(S_{ABC} = 3\) в формулу объема:
\(V = \frac{1}{3} \cdot 3 \cdot 1 = 1\)
Получаем V = 1, что соответствует условию задачи.

Ответ: площадь основания пирамиды SABC равна 3 квадратным единицам.