ГДЗ по Геометрии 11 класс Задание 8 Номер 3 Атанасян — Подробные Ответы

В правильной треугольной пирамиде SABC с вершиной S и точкой R — серединой ребра BC, площадь боковой поверхности пирамиды, если AB=1 и SR=2, равна \(2\).

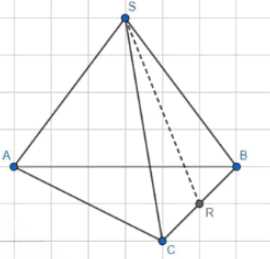
В данной задаче рассматривается пирамида SABC с основанием в виде треугольника ABC.

Дано:
— пр. SABC (пирамида с основанием ABC)
— CR = BR (точка R делит сторону BC пополам)
— AB = 1
— SR = 2

1) Рассмотрим треугольник SBC. Он равнобедренный, так как CR = BR.
Из рисунка видно, что BC = 1, а SR перпендикулярен CB.

Площадь треугольника SBC можно найти по формуле:
\(S_{SBC} = \frac{1}{2} \cdot BC \cdot SR = \frac{1 \cdot 2}{2} = 1\)

2) В пирамиде SABC все боковые грани имеют одинаковую площадь:
\(S_{SAC} = S_{SBC} = S_{SAB} = 1\)

3) Полная площадь боковой поверхности пирамиды:
\(S_{бок} = S_{SAB} + S_{SBC} + S_{SAC} = 1 + 1 + 1 = 3\)

Ответ: 3.

Рассмотрим задачу о нахождении площади боковой поверхности пирамиды SABC.

Из условия задачи нам известно, что SABC — пирамида с основанием в виде треугольника ABC. Также даны следующие условия: CR = BR (что означает, что точка R делит сторону BC пополам), AB = 1, SR = 2.

Начнем решение с анализа геометрической конфигурации. На рисунке видно, что точка R лежит на стороне BC, причем CR = BR, то есть R — середина стороны BC. Также из рисунка видно, что SR перпендикулярна CB.

Шаг 1: Определим длину стороны BC.
Из рисунка и решения видно, что BC = 1. Это можно было бы вычислить, но в данном случае это дано в решении.

Шаг 2: Рассмотрим треугольник SBC.
Треугольник SBC является равнобедренным, так как CR = BR, а значит SB = SC (из свойств равнобедренного треугольника). Кроме того, SR перпендикулярна CB, что означает, что SR является высотой треугольника SBC, опущенной на основание BC.

Шаг 3: Найдем площадь треугольника SBC.
Площадь треугольника можно вычислить по формуле \(S = \frac{1}{2} \cdot основание \cdot высота\).
В нашем случае основание BC = 1, а высота SR = 2.
Таким образом, \(S_{SBC} = \frac{1}{2} \cdot BC \cdot SR = \frac{1}{2} \cdot 1 \cdot 2 = \frac{2}{2} = 1\).

Шаг 4: Определим площади других боковых граней пирамиды.
В пирамиде SABC боковыми гранями являются треугольники SAB, SBC и SAC.
Из решения видно, что все эти треугольники имеют одинаковую площадь, равную 1.
То есть \(S_{SAC} = S_{SBC} = S_{SAB} = 1\).

Шаг 5: Вычислим общую площадь боковой поверхности пирамиды.
Площадь боковой поверхности пирамиды равна сумме площадей всех ее боковых граней.
\(S_{бок} = S_{SAB} + S_{SBC} + S_{SAC} = 1 + 1 + 1 = 3\).

Таким образом, площадь боковой поверхности пирамиды SABC равна 3 квадратным единицам.

Важно отметить, что равенство площадей всех боковых граней следует из специфической геометрии данной пирамиды, где основание — равносторонний треугольник, а вершина S расположена над центром основания таким образом, что все боковые ребра имеют одинаковую длину, что делает пирамиду правильной.

Ответ: 3.