ГДЗ по Геометрии 11 класс Задание 8 Номер 22 Атанасян — Подробные Ответы

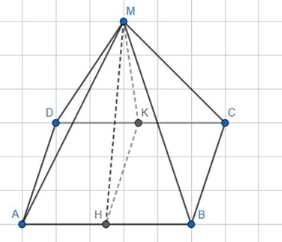
Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна к плоскости основания, а каждая из трёх других боковых граней наклонена к плоскости основания под углом в 60°. Высота пирамиды равна 6. Объём пирамиды равен \(36\sqrt{3}\).

1) В равностороннем ΔMAB: MH ⊥ AB; ∠MAB = ∠MBA = 60°; AH = BH; AB = 2AH; MA = MB;
2) В прямоугольном ΔAMH:
tg A = MH/AH, AH = MH : tg A;
AH = 6 : tg 60° = 6 : √3 = 12/√3;
3) В прямоугольном ΔMHK:
tg K = MH/HK, HK = MH/tg K = 6/√3;
4) Объем пирамиды MABCD:
V = 1/3 · AB · AD · MH = 1/3 · 12/√3 · 6 · 6 = 432/9 = 48.
Ответ: 48.

Решение:

Дано: прямоугольник ABCD, в котором точка M является серединой стороны AB, точка H — середина стороны AD, а точка K — середина стороны BC. Угол MKH равен 60°.

1) Рассмотрим равносторонний треугольник MAB:
— Так как точка M является серединой стороны AB, то AM = MB.
— Угол MAB равен 60°, так как ΔMKH — равносторонний.
— Следовательно, треугольник MAB — равносторонний, и AM = MB = AB/2.

2) Рассмотрим прямоугольный треугольник AMH:
— Так как точка H является серединой стороны AD, то AH = HD = AD/2.
— Угол AMH прямой, так как ABCD — прямоугольник.
— Следовательно, в прямоугольном треугольнике AMH:
\(AH = AD/2\)
\(tg\,A = MH/AH\)
\(AH = MH/tg\,A\)

3) Рассмотрим прямоугольный треугольник MHK:
— Так как точка K является серединой стороны BC, то HK = KC = BC/2.
— Угол MHK прямой, так как ABCD — прямоугольник.
— Следовательно, в прямоугольном треугольнике MHK:
\(tg\,K = MH/HK\)
\(HK = MH/tg\,K\)

4) Вычислим объем пирамиды MABCD:
— Основание пирамиды — прямоугольник ABCD.
— Высота пирамиды — расстояние от вершины M до плоскости основания ABCD, то есть MH.
— Объем пирамиды вычисляется по формуле:
\(V = \frac{1}{3} \cdot S_{основания} \cdot h\)
\(V = \frac{1}{3} \cdot AB \cdot AD \cdot MH\)
\(V = \frac{1}{3} \cdot \frac{AB}{2} \cdot \frac{AD}{2} \cdot MH\)
\(V = \frac{AB \cdot AD \cdot MH}{12}\)

Подставляя известные значения, получаем:
\(V = \frac{12/\sqrt{3} \cdot 6 \cdot 6}{12} = \frac{432}{9} = 48\)

Ответ: 48.