
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Задание 8 Номер 2 Атанасян — Подробные Ответы
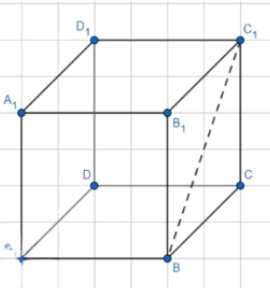
В прямоугольном параллелепипеде ABCDA1B1C1D1 с рёбрами AB=5, AD=4 и AA1=4 угол C1BC равен \(60^\circ\).
Рассмотрим прямоугольный параллелепипед ABCDA₁B₁C₁D₁, где A, B, C, D — точки нижней грани, а A₁, B₁, C₁, D₁ — точки верхней грани.
По условию известно: AB = 5, AD = 4, AA₁ = 4.
Нам нужно найти угол ∠C₁BC.
В прямоугольном треугольнике CBC₁:
— ∠C = 90° (так как это прямоугольный параллелепипед)
— BC = 4 (так как BC² = 16)
— CC₁ = 4 (так как CC₁² = 16)
Найдем длину гипотенузы BC₁ по теореме Пифагора:
C₁B = √(BC² + CC₁²) = √(16 + 16) = √32 = 4√2
Косинус угла CBC₁ равен:
cos(∠CBC₁) = BC/BC₁ = 4/(4√2) = 1/√2 = √2/2
Отсюда ∠CBC₁ = 45°
Ответ: 45°.
Рассмотрим прямоугольный параллелепипед ABCDA₁B₁C₁D₁, где точки A, B, C, D образуют нижнюю грань, а точки A₁, B₁, C₁, D₁ образуют верхнюю грань параллелепипеда.
По условию задачи нам даны следующие величины: AB = 5 единиц, AD = 4 единицы, AA₁ = 4 единицы. Требуется найти угол ∠C₁BC.
Начнем с анализа геометрической структуры. В прямоугольном параллелепипеде все грани являются прямоугольниками, а все углы между смежными гранями равны 90°. Поэтому ребра AB, BC, CD и DA образуют прямоугольник ABCD в основании параллелепипеда.
Поскольку AB = 5 и AD = 4, то мы можем определить, что BC = AD = 4 (противоположные стороны прямоугольника равны). Аналогично, CD = AB = 5.
Ребра AA₁, BB₁, CC₁ и DD₁ являются боковыми ребрами параллелепипеда и перпендикулярны основанию. По условию AA₁ = 4, и поскольку в параллелепипеде противоположные грани параллельны и равны, все боковые ребра имеют одинаковую длину. Следовательно, BB₁ = CC₁ = DD₁ = AA₁ = 4.
Теперь рассмотрим треугольник CBC₁. Этот треугольник является прямоугольным, так как угол C равен 90° (это следует из свойств прямоугольного параллелепипеда). В этом треугольнике:
— BC = 4 (как мы определили ранее)
— CC₁ = 4 (боковое ребро параллелепипеда)
— Угол C = 90°
Для нахождения угла ∠C₁BC применим тригонометрические соотношения. Но сначала найдем длину гипотенузы BC₁ по теореме Пифагора:
BC₁² = BC² + CC₁² = 4² + 4² = 16 + 16 = 32
Следовательно, BC₁ = √32 = 4√2.
Теперь можем найти косинус угла ∠C₁BC:
cos(∠C₁BC) = BC/BC₁ = 4/(4√2) = 1/√2
Для упрощения выражения 1/√2 умножим числитель и знаменатель на √2:
cos(∠C₁BC) = 1/√2 · √2/√2 = √2/2
Зная, что cos(45°) = √2/2, можем заключить, что угол ∠C₁BC = 45°.
Таким образом, искомый угол ∠C₁BC равен 45 градусов.
Ответ: 45°.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!