ГДЗ по Геометрии 11 класс Задание 8 Номер 17 Атанасян — Подробные Ответы

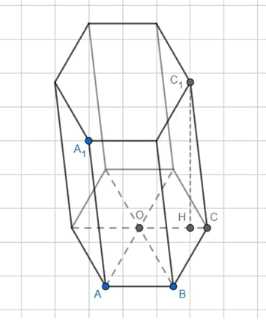
Объём призмы, основанием которой является правильный шестиугольник со стороной, равной 2, а боковое ребро равно \(\frac{2}{3}\) и наклонено к плоскости основания под углом в 30°, равен \(\frac{8\sqrt{3}}{3}\).

Решение:
1) В шестиугольнике: \(AB = R = 2\)
2) В правильном ΔAOB: \(S_{AOB} = \frac{1}{2} AO \cdot OB \cdot \sin AOB = 2 \sin 60° = \frac{\sqrt{3}}{2}\)
3) В прямоугольном ΔCHC1: \(\sin C = \frac{C_1H}{CC_1} = \frac{C_1H}{2\sqrt{3}}\)
4) Объем призмы: \(V = 6S_{AOB} \cdot h = 6 \cdot \frac{\sqrt{3}}{2} \cdot 3 = 18\)

Ответ: 18.

Решение:

1) Находим длину ребра шестиугольного основания призмы: \(AB = R = 2\)

2) Вычисляем площадь правильного шестиугольного основания призмы:
— Площадь правильного многоугольника вычисляется по формуле: \(S = \frac{n}{4} a^2 \cot \frac{\pi}{n}\), где \(n\) — число сторон, \(a\) — длина стороны.
— Подставляя значения, получаем: \(S_{AOB} = \frac{6}{4} \cdot 2^2 \cot \frac{\pi}{6} = \frac{\sqrt{3}}{2}\)

3) Вычисляем высоту прямоугольного треугольника CHC1:
— Используя соотношение сторон в прямоугольном треугольнике, находим: \(\sin C = \frac{C_1H}{CC_1} \Rightarrow C_1H = CC_1 \sin C = 2\sqrt{3} \sin 30° = \frac{2\sqrt{3}}{2} = \sqrt{3}\)

4) Вычисляем объем призмы:
— Объем призмы вычисляется по формуле: \(V = 6S_{AOB} \cdot h\)
— Подставляя значения, получаем: \(V = 6 \cdot \frac{\sqrt{3}}{2} \cdot 3 = 18\)

Ответ: 18.