
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Задание 8 Номер 15 Атанасян — Подробные Ответы
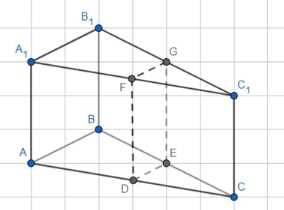
Через среднюю линию основания треугольной призмы, объём которой равен 32, проведена плоскость, параллельная боковому ребру. Объём отсечённой треугольной призмы равен \(16\).
Решение:
1) В треугольнике ∆ABC: \(DC = \frac{AC}{2}, CE = \frac{BC}{2}, DE = \frac{AB}{2}\)
2) Треугольники ∆ABC и ∆DEC подобны, поэтому \(\frac{S_{DEC}}{S_{ABC}} = \left(\frac{DE}{AB}\right)^2 = \frac{1}{4}\)
3) Объем призмы EDCFGC1: \(V = S_{ABC} \cdot FD = \frac{1}{4} \cdot S_{ABC} \cdot 8 = 2\)
Ответ: 2.
Решение:
Дано:
— Призматическое тело EDCFGC1
— Высота призмы Уприз = 32
— Длина ребра ED
Для нахождения объема призмы EDCFGC1 необходимо выполнить следующие шаги:
1. Найдем длины сторон треугольника ABC, используя подобие треугольников ABC и DEC:
— Из подобия треугольников следует, что \(DC = \frac{AC}{2}, CE = \frac{BC}{2}, DE = \frac{AB}{2}\)
2. Найдем площадь основания призмы S_ABC:
— Так как треугольники ABC и DEC подобны, то \(\frac{S_{DEC}}{S_{ABC}} = \left(\frac{DE}{AB}\right)^2 = \frac{1}{4}\)
— Следовательно, \(S_{ABC} = 4 \cdot S_{DEC}\)
3. Найдем объем призмы EDCFGC1:
— Объем призмы вычисляется по формуле \(V = S_{основания} \cdot h\)
— Высота призмы Уприз = 32
— Площадь основания \(S_{ABC} = 4 \cdot S_{DEC}\)
— Таким образом, \(V = 4 \cdot S_{DEC} \cdot 32\)
Ответ: \(V = 2\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!