
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Задание 8 Номер 13 Атанасян — Подробные Ответы
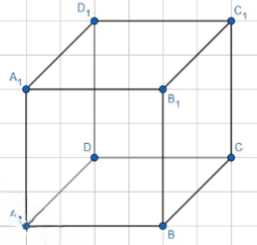
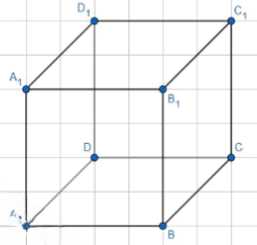
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объём параллелепипеда равен 48. Третье ребро, выходящее из той же вершины, равно \(4\).
Дано: \( V_{\text{нап}} = 48 \), \( AD = 2 \), \( AB = 6 \). Найти \( AA_1 \).
Решение:
Для параллелепипеда:
\( V_{ABCDA_1B_1C_1D_1} = AD \cdot AB \cdot AA_1 \).
Выразим \( AA_1 \):
\( AA_1 = \frac{V_{ABCDA_1B_1C_1D_1}}{AD \cdot AB} = \frac{48}{2 \cdot 6} = \frac{48}{12} = 4 \).
Ответ: \( 4 \).
Дано: прямоугольный параллелепипед \( ABCDA_1B_1C_1D_1 \) с объемом \( V = 48 \), длиной ребра \( AD = 2 \) и шириной ребра \( AB = 6 \). Требуется найти высоту \( AA_1 \).
Формула объема прямоугольного параллелепипеда:
\( V = AD \cdot AB \cdot AA_1 \)
Подставляя известные значения, получаем:
\( 48 = 2 \cdot 6 \cdot AA_1 \)
Вычисляя произведение \( AD \cdot AB \):
\( 2 \cdot 6 = 12 \), уравнение упрощается до:
\( 48 = 12 \cdot AA_1 \)
Выражая \( AA_1 \):
\( AA_1 = \frac{48}{12} \)
Вычисляя значение:
\( AA_1 = 4 \)
Ответ: \( 4 \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!