
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Задание 8 Номер 1 Атанасян — Подробные Ответы
Квадрат расстояния между вершинами D и B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB=3, AD=8 и AA1=5, равен \(25\).
Решение:
1) В прямоугольном ΔADB: \(\angle A = 90^\circ\), \(AB^2 = 9\), \(AD^2 = 64\); \(BD^2 = AD^2 + BD^2 = 9 + 64 = 73\);
2) В прямоугольном ΔBDB1: \(\angle B = 90^\circ\), \(BB^2 = 25\), \(BD^2 = 73\); \(DB^2 = BD^2 + BB^2 = 73 + 25 = 98\).
Ответ: 98.
Дано: AB = 3; AD = 8; AA₁ = 5.
Найти: DB₁².
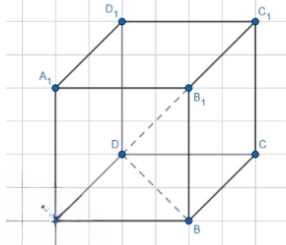
Рассмотрим задачу на рисунке. У нас есть куб ABCDA₁B₁C₁D₁, где точки A, B, C, D образуют нижнюю грань, а точки A₁, B₁, C₁, D₁ образуют верхнюю грань. Нам необходимо найти квадрат расстояния между точками D и B₁.
Для решения этой задачи воспользуемся координатным методом. Поместим начало координат в точку A, при этом оси направим вдоль рёбер куба: ось x вдоль AB, ось y вдоль AD, а ось z вдоль AA₁.
Тогда координаты точек будут следующие:
A(0, 0, 0)
B(3, 0, 0), так как AB = 3
D(0, 8, 0), так как AD = 8
A₁(0, 0, 5), так как AA₁ = 5
B₁(3, 0, 5), так как B₁ находится над B на высоте 5
Теперь найдём расстояние между точками D и B₁. Для этого используем формулу расстояния между двумя точками в пространстве:
\(DB₁² = (x_{B₁} — x_D)² + (y_{B₁} — y_D)² + (z_{B₁} — z_D)²\)
Подставляем координаты:
\(DB₁² = (3 — 0)² + (0 — 8)² + (5 — 0)²\)
\(DB₁² = 9 + 64 + 25\)
\(DB₁² = 98\)
Можно решить эту задачу и другим способом, используя теорему Пифагора дважды:
1) Сначала рассмотрим прямоугольный треугольник ΔADB:
\(\angle A = 90°\) (так как это прямой угол в кубе)
\(AB² = 3² = 9\)
\(AD² = 8² = 64\)
По теореме Пифагора:
\(BD² = AB² + AD² = 9 + 64 = 73\)
2) Затем рассмотрим прямоугольный треугольник ΔBDB₁:
\(\angle B = 90°\) (так как это прямой угол в кубе)
\(BB₁² = 5² = 25\) (так как BB₁ = AA₁ = 5, как противоположные рёбра куба)
\(BD² = 73\) (найдено в предыдущем шаге)
По теореме Пифагора:
\(DB₁² = BD² + BB₁² = 73 + 25 = 98\)
Таким образом, квадрат расстояния между точками D и B₁ равен 98.
Ответ: DB₁² = 98.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!