ГДЗ по Геометрии 11 класс Задание 3 Номер 3 Атанасян — Подробные Ответы

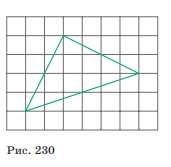
Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см х 1 см (рис. 230).

Решение:

1) В прямоугольном ΔADB: ∠D = 90°, AD = 4, BD = 2; S_ADB = \(\frac{1}{2}\)AD·DB = 2·2 = 4;

2) В прямоугольном ΔBEC: ∠E = 90°, BE = 4, CE = 2; S_BEC = \(\frac{1}{2}\)BE·CE = 2·2 = 4;

3) В прямоугольном ΔACF: ∠F = 90°, AF = 6, CF = 2; S_ACF = \(\frac{1}{2}\)AF·CF = 3·2 = 6;

4) В прямоугольнике ΔADEF: S_ADEF = AF·EF = 4·6 = 24;

5) В треугольнике ΔABC: S = 24 — 4 — 4 — 6 = 10.

Ответ: 10 см².

Решение:

Дано: треугольник ΔABC. Требуется найти его площадь S_ABC.

Для решения этой задачи будем использовать свойства прямоугольных треугольников, содержащихся в данном треугольнике.

1) Рассмотрим прямоугольный треугольник ΔADB:
— Угол ∠D равен 90°, так как он является прямым углом.
— Катет AD равен 4, а катет BD равен 2.
— Площадь этого треугольника вычисляется по формуле: S_ADB = \(\frac{1}{2}\)·AD·DB = \(\frac{1}{2}\)·4·2 = 4.

2) Рассмотрим прямоугольный треугольник ΔBEC:
— Угол ∠E равен 90°, так как он является прямым углом.
— Катет BE равен 4, а катет CE равен 2.
— Площадь этого треугольника вычисляется по формуле: S_BEC = \(\frac{1}{2}\)·BE·CE = \(\frac{1}{2}\)·4·2 = 4.

3) Рассмотрим прямоугольный треугольник ΔACF:
— Угол ∠F равен 90°, так как он является прямым углом.
— Катет AF равен 6, а катет CF равен 2.
— Площадь этого треугольника вычисляется по формуле: S_ACF = \(\frac{1}{2}\)·AF·CF = \(\frac{1}{2}\)·6·2 = 6.

4) Рассмотрим прямоугольник ΔADEF:
— Стороны AF и EF равны 4 и 6 соответственно.
— Площадь этого прямоугольника вычисляется по формуле: S_ADEF = AF·EF = 4·6 = 24.

5) Площадь треугольника ΔABC вычисляется как разность площадей прямоугольника ΔADEF и суммы площадей треугольников ΔADB, ΔBEC и ΔACF:
S_ABC = S_ADEF — (S_ADB + S_BEC + S_ACF) = 24 — (4 + 4 + 6) = 10.

Ответ: 10 см².