ГДЗ по Геометрии 11 класс Задание 3 Номер 14 Атанасян — Подробные Ответы

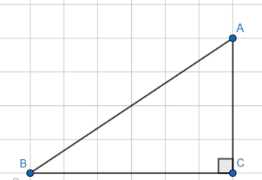
Площадь прямоугольного треугольника равна 12, а один из его катетов равен 6. Найдите другой катет.

В прямоугольном треугольнике ABC с прямым углом C площадь вычисляется по формуле \(S_{ABC} = \frac{1}{2} \cdot BC \cdot AC\). Дано, что \(S_{ABC} = 12\) и \(BC = 6\). Подставляя известные значения в формулу, получаем \(12 = \frac{1}{2} \cdot 6 \cdot AC\). Упрощая, имеем \(12 = 3 \cdot AC\). Чтобы найти AC, разделим обе стороны на 3: \(AC = \frac{12}{3}\), что дает \(AC = 4\). Ответ: 4.

Дано, что треугольник ABC является прямоугольным с прямым углом при вершине C, то есть \(\angle C = 90^\circ\). Также известна площадь этого треугольника, \(S_{ABC} = 12\), и длина одной из сторон, образующих прямой угол, \(BC = 6\). Требуется найти длину другой стороны, образующей прямой угол, а именно AC.

Площадь прямоугольного треугольника равна половине произведения длин его катетов (сторон, образующих прямой угол). В данном треугольнике ABC катетами являются стороны BC и AC. Следовательно, формула для площади треугольника ABC может быть записана как \(S_{ABC} = \frac{1}{2} \cdot BC \cdot AC\).

Теперь подставим известные значения в эту формулу. Нам дано, что \(S_{ABC} = 12\) и \(BC = 6\). Получаем уравнение: \(12 = \frac{1}{2} \cdot 6 \cdot AC\).

Далее упростим правую часть уравнения. Произведение \(\frac{1}{2} \cdot 6\) равно 3. Таким образом, уравнение принимает вид: \(12 = 3 \cdot AC\).

Чтобы найти длину стороны AC, необходимо разделить обе части этого уравнения на коэффициент при AC, который равен 3. Выполняя деление, получаем: \(AC = \frac{12}{3}\).

Вычисляя значение дроби, находим \(AC = 4\).

Таким образом, длина стороны AC равна 4.

Ответ: 4.