
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Задание 3 Номер 10 Атанасян — Подробные Ответы
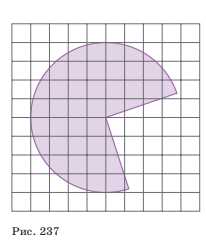
Найдите площадь \(S\) части круга, изображённой на клетчатой бумаге с размером клетки 1 см х 1 см (рис. 237). В ответе укажите число, равное \(\frac{S}{\pi}\).
Решение:
1) Треугольники равны: \(OA = CD = 3\), \(AB = OD = 1\); \(\angle A = \angle ZD = 90^\circ\); \(\angle AOD = \angle AOB\); \(\angle BOC = \angle BOA + \angle DOC = 90^\circ\)
2) Площадь сектора круга: \(R = 4\), \(S_{сек} = S — \frac{1}{4} \cdot S = \frac{3}{4} S\), \(S_{сек} = \frac{3}{4} \pi R^2 = \frac{3}{4} \pi \cdot 16 = 12\pi\)
Ответ: 12.
Дано: сектор круга с радиусом \(R = 4\).
Решение:
1) Треугольники \(\triangle OAB\) и \(\triangle ODC\) равны, так как они имеют одинаковые стороны: \(OA = CD = 3\) и \(AB = OD = 1\).
2) Так как \(\angle A = \angle ZD = 90^\circ\), то \(\angle AOD = \angle AOB\).
3) Так как \(\angle BOC = \angle BOA + \angle DOC = 90^\circ\), то треугольники \(\triangle BOC\) и \(\triangle BOA\) вместе образуют прямой угол.
4) Площадь сектора круга \(S_{сек}\) можно найти как разность площади круга \(S = \pi R^2\) и площади треугольника \(\triangle AOB\):
\(S_{сек} = S — \frac{1}{4} \cdot S = \frac{3}{4} \cdot \pi R^2 = \frac{3}{4} \cdot \pi \cdot 16 = 12\pi\)
Ответ: 12.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!