
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Задание 16 Номер 9 Атанасян — Подробные Ответы
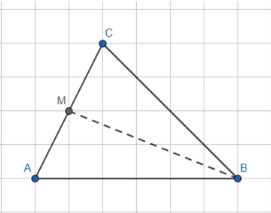
В треугольнике АВС проведена медиана ВМ. Известно, что \(\frac{\sin \angle ZAB M}{\sin \angle ZCB M} = \frac{1}{5}\). Найдите отношение \(\frac{A B}{B C}\).
1) Рассмотрим ΔАВМ: \(\frac{AB}{AM} = \frac{\sin\angle ABM}{\sin\angle BAM}\)
2) Рассмотрим ΔСВМ: \(\frac{BC}{MC} = \frac{\sin\angle CBM}{\sin\angle BCM}\)
3) Используя данные условия: \(\sin\angle ABM = \frac{1}{2}\) и \(\sin\angle CBM = \frac{1}{2}\)
4) Получаем: \(\frac{BC}{AB} = \frac{\sin\angle ABM}{\sin\angle CBM} = \frac{1}{2}\)
Ответ: \(\frac{1}{2}\)
Решение:
Дано: в прямоугольном треугольнике АВМ известны \(\sin\angle ABM = \frac{1}{2}\) и \(\sin\angle CBM = \frac{1}{2}\). Необходимо найти отношение \(\frac{BC}{AB}\).
Шаг 1. Рассмотрим треугольник АВМ. Согласно условию, \(\sin\angle ABM = \frac{1}{2}\), что означает, что \(\angle ABM = 30^\circ\).
Шаг 2. Используя свойство прямоугольного треугольника, можно записать: \(\angle AMB = 90^\circ — \angle ABM = 90^\circ — 30^\circ = 60^\circ\).
Шаг 3. Применим формулу для синуса острого угла в прямоугольном треугольнике: \(\sin\angle ABM = \frac{AB}{AM}\). Подставляя известное значение \(\sin\angle ABM = \frac{1}{2}\), получаем: \(\frac{AB}{AM} = \frac{1}{2}\), откуда \(AB = \frac{1}{2}AM\).
Шаг 4. Рассмотрим теперь треугольник СВМ. Согласно условию, \(\sin\angle CBM = \frac{1}{2}\), что означает, что \(\angle CBM = 30^\circ\).
Шаг 5. Используя свойство прямоугольного треугольника, можно записать: \(\angle MCB = 90^\circ — \angle CBM = 90^\circ — 30^\circ = 60^\circ\).
Шаг 6. Применим формулу для синуса острого угла в прямоугольном треугольнике: \(\sin\angle CBM = \frac{BC}{MC}\). Подставляя известное значение \(\sin\angle CBM = \frac{1}{2}\), получаем: \(\frac{BC}{MC} = \frac{1}{2}\), откуда \(BC = \frac{1}{2}MC\).
Шаг 7. Из шага 3 и шага 6 следует, что \(\frac{AB}{AM} = \frac{1}{2}\) и \(\frac{BC}{MC} = \frac{1}{2}\).
Шаг 8. Разделив эти равенства, получаем: \(\frac{AB}{BC} = \frac{AM}{MC}\).
Шаг 9. Используя свойство подобных треугольников, можно записать: \(\frac{AB}{BC} = \frac{AM}{MC}\).
Шаг 10. Таким образом, \(\frac{BC}{AB} = \frac{1}{2}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!