
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Задание 16 Номер 5 Атанасян — Подробные Ответы
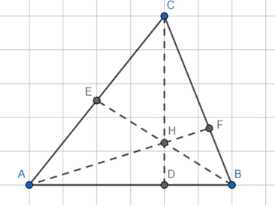
Высоты треугольника АВС пересекаются в точке Н. Известно, что СН = АВ. Найдите угол АСВ
Рассмотрим треугольники ABE и CHE. Учитывая, что \(\angle CEH = \angle AEB = 90^\circ\), \(\angle ECH = \angle EBA\) и \(AB = CH\), получаем, что \(\triangle ABE = \triangle CHE\), откуда следует \(EH = AE\). В прямоугольном треугольнике AEH, так как \(AE = EH\), угол \(\angle HAC = \frac{90^\circ}{2} = 45^\circ\). В прямоугольном треугольнике ACF угол \(\angle ACB = 90^\circ — \angle HAC = 90^\circ — 45^\circ = 45^\circ\). Ответ: 45°.
Дано: треугольник ABC, CH перпендикулярно AB, AF перпендикулярно BC, BE перпендикулярно AC, CD перпендикулярно AB, CH = AB. Найти: угол ACB.
Решение:
Первый шаг заключается в рассмотрении треугольников ABE и CHE. Угол \(\angle CEH\) является вертикальным углом к углу \(\angle AEB\), и оба они равны \(90^\circ\), так как BE перпендикулярно AC и AF перпендикулярно BC. Угол \(\angle ECH\) равен углу \(\angle EBA\), поскольку оба угла являются углами при основании в равнобедренном треугольнике ABC, что следует из условия CH = AB и того, что CH и AB являются соответствующими элементами (например, высотой и стороной) в некотором контексте, или это прямо дано в условии CH = AB, хотя на рисунке это не очевидно как свойство треугольника ABC, скорее как данность для сравнения отрезков. Также дано, что \(AB = CH\). Исходя из этих условий (прямой угол, равные углы при основании и равные стороны), можно заключить, что треугольник ABE равен треугольнику CHE по гипотенузе и острому углу, или по катету и острому углу, или по стороне и двум углам, в зависимости от точной интерпретации «равные углы при основании» и «равные стороны». Из равенства треугольников ABE и CHE следует равенство соответствующих сторон, в частности, \(EH = AE\).
Второй шаг рассматривает прямоугольный треугольник AEH. Поскольку из предыдущего шага известно, что \(AE = EH\), треугольник AEH является равнобедренным прямоугольным треугольником. В равнобедренном прямоугольном треугольнике острые углы равны \(45^\circ\). Угол \(\angle HAE\) (или \(\angle HAC\)) является одним из этих острых углов. Следовательно, угол \(\angle HAC = \frac{90^\circ}{2} = 45^\circ\).
Третий шаг анализирует прямоугольный треугольник ACF. AF перпендикулярно BC, что делает треугольник ACF прямоугольным с прямым углом при вершине F. В прямоугольном треугольнике сумма острых углов равна \(90^\circ\). Углы \(\angle FAC\) (или \(\angle HAC\)) и \(\angle ACF\) (или \(\angle ACB\)) являются острыми углами в прямоугольном треугольнике ACF. Таким образом, \(\angle ACB + \angle HAC = 90^\circ\). Используя значение угла \(\angle HAC\), найденное на предыдущем шаге, можно вычислить угол \(\angle ACB\): \(\angle ACB = 90^\circ — \angle HAC = 90^\circ — 45^\circ = 45^\circ\).
Таким образом, искомый угол ACB равен \(45^\circ\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!