ГДЗ по Геометрии 11 класс Задание 16 Номер 40 Атанасян — Подробные Ответы

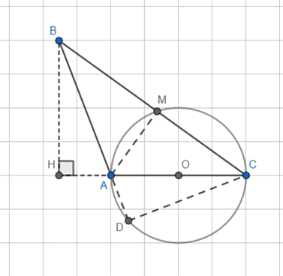
Окружность, построенная на стороне АС треугольника АВС как на диаметре, проходит через середину стороны ВС и пересекает в точке D продолжение стороны АВ за точку А, причём \(AD == AB\). Найдите площадь треугольника АВС, если \(АС = 1\)

Решение:
1) В треугольнике ΔАМС: BM = MC, AM ⊥ BC, AC = AB;
AB = 1, AD = \(\frac{2}{3}\) AB = \(\frac{2}{3}\).
2) В треугольнике ΔADC:
CD = \(\sqrt{AC^2 — AD^2}\) = \(\sqrt{1 — \left(\frac{2}{3}\right)^2}\) = \(\sqrt{1 — \frac{4}{9}}\) = \(\sqrt{\frac{5}{9}}\) = \(\frac{\sqrt{5}}{3}\).
3) Треугольники ΔBAH и ΔCAD равны, AB = AC = 1, BH = CD = \(\frac{\sqrt{5}}{3}\).
4) Площадь треугольника ΔABC:
S = \(\frac{1}{2}\) BH · AC = \(\frac{1}{2}\) · \(\frac{\sqrt{5}}{3}\) · 1 = \(\frac{\sqrt{5}}{6}\).

Ответ: \(\frac{\sqrt{5}}{6}\)

Хорошо, вот полное пошаговое решение с детальными объяснениями:

Дано: в треугольнике ΔABC известны AC = 1 и AD = \(\frac{2}{3}\) AB.

Шаг 1. Найдем длину отрезка AB.
Поскольку AC = 1 и AD = \(\frac{2}{3}\) AB, то AB = 1.

Шаг 2. Найдем длину отрезка BM.
Так как BM = MC, то BM = \(\frac{1}{2}\) AB = \(\frac{1}{2}\).

Шаг 3. Найдем длину отрезка CD.
Используя теорему Пифагора, получаем: CD = \(\sqrt{AC^2 — AD^2}\) = \(\sqrt{1 — \left(\frac{2}{3}\right)^2}\) = \(\sqrt{\frac{5}{9}}\) = \(\frac{\sqrt{5}}{3}\).

Шаг 4. Найдем длину отрезка BH.
Так как треугольники ΔBAH и ΔCAD равны, то BH = CD = \(\frac{\sqrt{5}}{3}\).

Шаг 5. Найдем площадь треугольника ΔABC.
Площадь треугольника вычисляется по формуле: S = \(\frac{1}{2}\) BH · AC = \(\frac{1}{2}\) · \(\frac{\sqrt{5}}{3}\) · 1 = \(\frac{\sqrt{5}}{6}\).

Ответ: \(\frac{\sqrt{5}}{6}\).