ГДЗ по Геометрии 11 класс Задание 16 Номер 4 Атанасян — Подробные Ответы

Две стороны треугольника равны 3 и 6, а угол между ними равен 60°. Найдите биссектрису треугольника, проведенную из вершины этого угла.

В треугольнике \( \triangle ACB \) по свойству биссектрисы \( CD \) имеем \( \frac{AD}{BD} = \frac{AC}{BC} = \frac{3}{6} = \frac{1}{2} \), откуда \( AD = \frac{1}{2} BD \).
По теореме косинусов для \( \triangle ACB \): \( AB^2 = AC^2 + BC^2 — 2 \cdot AC \cdot BC \cdot \cos(\angle C) \).
\( AB^2 = 3^2 + 6^2 — 2 \cdot 3 \cdot 6 \cdot \cos(60^\circ) = 9 + 36 — 36 \cdot \frac{1}{2} = 45 — 18 = 27 \).
\( AB = \sqrt{27} = 3\sqrt{3} \).
Так как \( AD = \frac{1}{2} BD \) и \( AD + BD = AB \), то \( \frac{1}{2} BD + BD = 3\sqrt{3} \), \( \frac{3}{2} BD = 3\sqrt{3} \), \( BD = 2\sqrt{3} \), и \( AD = \frac{1}{2} \cdot 2\sqrt{3} = \sqrt{3} \).
В треугольнике \( \triangle ACD \) по теореме косинусов: \( AD^2 = AC^2 + CD^2 — 2 \cdot AC \cdot CD \cdot \cos(\angle ACD) \).
Так как \( CD \) биссектриса \( \angle C = 60^\circ \), то \( \angle ACD = \frac{60^\circ}{2} = 30^\circ \).
\( (\sqrt{3})^2 = 3^2 + CD^2 — 2 \cdot 3 \cdot CD \cdot \cos(30^\circ) \).
\( 3 = 9 + CD^2 — 6 \cdot CD \cdot \frac{\sqrt{3}}{2} \).
\( 3 = 9 + CD^2 — 3\sqrt{3} CD \).
\( CD^2 — 3\sqrt{3} CD + 6 = 0 \).
Решим квадратное уравнение относительно \( CD \). Дискриминант \( D = (-3\sqrt{3})^2 — 4 \cdot 1 \cdot 6 = 27 — 24 = 3 \).
Корни: \( CD = \frac{-(-3\sqrt{3}) \pm \sqrt{3}}{2 \cdot 1} = \frac{3\sqrt{3} \pm \sqrt{3}}{2} \).
\( CD_1 = \frac{3\sqrt{3} + \sqrt{3}}{2} = \frac{4\sqrt{3}}{2} = 2\sqrt{3} \).
\( CD_2 = \frac{3\sqrt{3} — \sqrt{3}}{2} = \frac{2\sqrt{3}}{2} = \sqrt{3} \).
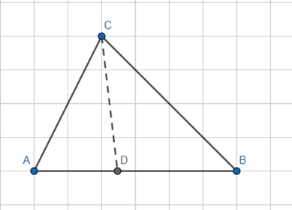
Поскольку \( AD = \sqrt{3} \), то \( CD \) не может быть равен \( \sqrt{3} \) (из рисунка видно, что \( CD > AD \)).
Следовательно, \( CD = 2\sqrt{3} \).
Ответ: \( 2\sqrt{3} \).

Дано: \( \triangle ABC \), \( CD \) — биссектриса угла \( C \), \( \angle C = 60^\circ \), \( AC = 3 \), \( CB = 6 \). Найти: \( CD \).

Применим свойство биссектрисы угла треугольника к биссектрисе \( CD \) в треугольнике \( \triangle ACB \). Оно гласит, что биссектриса делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам. То есть, \( \frac{AD}{BD} = \frac{AC}{BC} \). Подставляя известные значения, получаем \( \frac{AD}{BD} = \frac{3}{6} = \frac{1}{2} \). Из этого соотношения следует, что \( AD = \frac{1}{2} BD \).

Найдем длину стороны \( AB \) в треугольнике \( \triangle ACB \) с помощью теоремы косинусов. Формула теоремы косинусов для стороны \( AB \) в \( \triangle ACB \) имеет вид \( AB^2 = AC^2 + BC^2 — 2 \cdot AC \cdot BC \cdot \cos(\angle C) \). Подставим данные значения: \( AB^2 = 3^2 + 6^2 — 2 \cdot 3 \cdot 6 \cdot \cos(60^\circ) \). Вычисляем квадраты сторон: \( AB^2 = 9 + 36 — 36 \cdot \cos(60^\circ) \). Значение косинуса \( \cos(60^\circ) = \frac{1}{2} \). Продолжаем вычисление: \( AB^2 = 9 + 36 — 36 \cdot \frac{1}{2} = 45 — 18 = 27 \). Таким образом, \( AB = \sqrt{27} \). Упростим корень: \( \sqrt{27} = \sqrt{9 \cdot 3} = 3\sqrt{3} \). Следовательно, длина стороны \( AB = 3\sqrt{3} \).

Теперь, используя соотношение \( AD = \frac{1}{2} BD \) и тот факт, что \( AD + BD = AB \), мы можем найти длины отрезков \( AD \) и \( BD \). Заменим \( AD \) в сумме на \( \frac{1}{2} BD \): \( \frac{1}{2} BD + BD = 3\sqrt{3} \). Приведем подобные слагаемые: \( \frac{3}{2} BD = 3\sqrt{3} \). Чтобы найти \( BD \), умножим обе части уравнения на \( \frac{2}{3} \): \( BD = 3\sqrt{3} \cdot \frac{2}{3} = 2\sqrt{3} \). Теперь найдем \( AD \): \( AD = \frac{1}{2} BD = \frac{1}{2} \cdot 2\sqrt{3} = \sqrt{3} \).

Рассмотрим треугольник \( \triangle ACD \). Мы хотим найти длину стороны \( CD \). Для этого применим теорему косинусов к этому треугольнику относительно стороны \( AD \). Формула будет выглядеть так: \( AD^2 = AC^2 + CD^2 — 2 \cdot AC \cdot CD \cdot \cos(\angle ACD) \). Поскольку \( CD \) является биссектрисой угла \( C \), который равен \( 60^\circ \), угол \( \angle ACD \) равен половине угла \( C \): \( \angle ACD = \frac{\angle C}{2} = \frac{60^\circ}{2} = 30^\circ \).

Теперь подставим известные значения в формулу теоремы косинусов для \( \triangle ACD \): \( (\sqrt{3})^2 = 3^2 + CD^2 — 2 \cdot 3 \cdot CD \cdot \cos(30^\circ) \). Вычисляем квадраты и подставляем значение косинуса \( \cos(30^\circ) = \frac{\sqrt{3}}{2} \): \( 3 = 9 + CD^2 — 6 \cdot CD \cdot \frac{\sqrt{3}}{2} \). Упростим последнее слагаемое: \( 3 = 9 + CD^2 — 3\sqrt{3} CD \). Перенесем все слагаемые в одну сторону, чтобы получить квадратное уравнение относительно \( CD \): \( CD^2 — 3\sqrt{3} CD + 9 — 3 = 0 \), что дает \( CD^2 — 3\sqrt{3} CD + 6 = 0 \).

Решим это квадратное уравнение \( CD^2 — 3\sqrt{3} CD + 6 = 0 \) с помощью формулы для корней квадратного уравнения \( x = \frac{-b \pm \sqrt{D}}{2a} \), где \( D = b^2 — 4ac \). В нашем случае \( a=1 \), \( b = -3\sqrt{3} \), \( c=6 \). Вычислим дискриминант: \( D = (-3\sqrt{3})^2 — 4 \cdot 1 \cdot 6 = (9 \cdot 3) — 24 = 27 — 24 = 3 \). Теперь найдем корни для \( CD \): \( CD = \frac{-(-3\sqrt{3}) \pm \sqrt{3}}{2 \cdot 1} = \frac{3\sqrt{3} \pm \sqrt{3}}{2} \). Получаем два возможных значения для \( CD \):
Первый корень: \( CD_1 = \frac{3\sqrt{3} + \sqrt{3}}{2} = \frac{4\sqrt{3}}{2} = 2\sqrt{3} \).
Второй корень: \( CD_2 = \frac{3\sqrt{3} — \sqrt{3}}{2} = \frac{2\sqrt{3}}{2} = \sqrt{3} \).

У нас получилось два возможных значения для длины биссектрисы \( CD \). Однако, из рисунка видно, что отрезок \( CD \) длиннее отрезка \( AD \). Мы нашли, что \( AD = \sqrt{3} \). Сравнивая возможные значения \( CD \) с \( AD \), видим, что \( \sqrt{3} \) равно \( AD \), что противоречит визуальному представлению на рисунке и геометрическому смыслу (биссектриса обычно длиннее отрезка, который она образует на стороне, если только треугольник не вырожденный). Значение \( 2\sqrt{3} \) больше, чем \( \sqrt{3} \). Следовательно, единственно верным значением для длины биссектрисы \( CD \) является \( 2\sqrt{3} \).

Ответ: \( 2\sqrt{3} \).