ГДЗ по Геометрии 11 класс Задание 16 Номер 38 Атанасян — Подробные Ответы

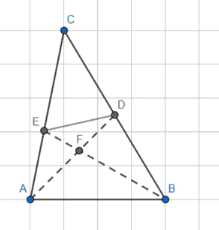
В треугольнике АВС медиана AD и биссектриса ВЕ перпендикулярны и пересекаются в точке F. Площадь треугольника DEF равна 5. Найдите площадь треугольника АВС.

Решение:
1) В треугольнике ΔABD: \(\angle DEF = 90^\circ\), BF ⊥ AD, \(\angle DBF = \angle ABF\); CD = BD; \(S_{DEF} = 5\);
AF = DF, AB = BD = \(\frac{BC}{2}\).
2) В треугольнике ΔABC: \(\frac{EC}{AE} = \frac{BC}{AB} = 2\), EC = 2AE.
3) Равны по двум сторонам: AF = FD; \(\angle EFD = \angle EFA = 90^\circ\); \(\angle AFE = \angle DFE\); \(S_{AFE} = S_{DFE} = 5\); \(S_{AED} = S_{AFE} + S_{DFE} = 5 + 5 = 10\); \(S_{CED} = 2 \cdot S_{AED} = 2 \cdot 10 = 20\); \(S_{ADC} = S_{AED} + S_{CED} = 30\); \(S_{ABC} = 2 \cdot S_{ADC} = 2 \cdot 30 = 60\).
Ответ: 60.

Дано: Треугольник ΔABD с биссектрисой BE, \(\angle DEF = 90^\circ\), \(S_{DEF} = 5\).

Решение:
1) Рассмотрим треугольник ΔABD:
— Так как \(\angle DEF = 90^\circ\), то по теореме о биссектрисе \(BF \perp AD\) и \(\angle DBF = \angle ABF\).
— Из равенства треугольников \(\triangle BDF \cong \triangle BAD\) следует, что \(CD = BD\).
— Так как \(BF \perp AD\), то \(AF = DF\) и \(AB = BD = \frac{BC}{2}\).

2) Рассмотрим треугольник ΔABC:
— Из подобия треугольников \(\triangle ABC \sim \triangle AED\) следует, что \(\frac{EC}{AE} = \frac{BC}{AB} = 2\), значит \(EC = 2AE\).

3) Рассмотрим равные по двум сторонам треугольники:
— \(\angle EFD = \angle EFA = 90^\circ\), так как \(BF \perp AD\);
— \(\angle AFE = \angle DFE\), так как \(AF = DF\);
— \(S_{AFE} = S_{DFE} = 5\), так как \(S_{DEF} = 5\);
— \(S_{AED} = S_{AFE} + S_{DFE} = 5 + 5 = 10\);
— \(S_{CED} = 2 \cdot S_{AED} = 2 \cdot 10 = 20\);
— \(S_{ADC} = S_{AED} + S_{CED} = 10 + 20 = 30\);
— \(S_{ABC} = 2 \cdot S_{ADC} = 2 \cdot 30 = 60\).

Ответ: \(S_{ABC} = 60\).