Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Задание 16 Номер 3 Атанасян — Подробные Ответы
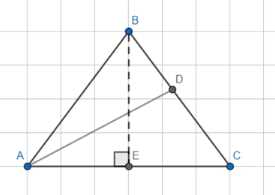
В равнобедренном треугольнике основание и боковая сторона равны соответственно 5 и 20. Найдите биссектрису, проведенную к боковой стороне треугольника.
В равнобедренном треугольнике \(ABC\) с \(AB = BC = 20\) и \(AC = 5\), \(AD\) — биссектриса угла \(A\). По свойству биссектрисы \(\frac{CD}{BD} = \frac{AC}{AB} = \frac{5}{20} = \frac{1}{4}\). Так как \(BD + CD = BC = 20\), имеем \(BD = 4CD\), откуда \(CD + 4CD = 20\), \(5CD = 20\), \(CD = 4\). В равнобедренном треугольнике \(ABC\), \(\cos C = \frac{AC/2}{BC} = \frac{5/2}{20} = \frac{5}{40} = \frac{1}{8}\). Применим теорему косинусов к треугольнику \(ADC\): \(AD^2 = AC^2 + CD^2 — 2 \cdot AC \cdot CD \cdot \cos C = 5^2 + 4^2 — 2 \cdot 5 \cdot 4 \cdot \frac{1}{8} = 25 +\)
\(+ 16 — \frac{40}{8} = 41 — 5 = 36\). Следовательно, \(AD = \sqrt{36} = 6\). Ответ: \(6\).
Дан равнобедренный треугольник \(ABC\), в котором стороны \(AB\) и \(BC\) равны \(20\), а сторона \(AC\) равна \(5\). \(AD\) является биссектрисой угла \(A\). Требуется найти длину биссектрисы \(AD\).
По свойству биссектрисы угла в треугольнике, биссектриса делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам. В нашем случае, биссектриса \(AD\) угла \(A\) делит сторону \(BC\) на отрезки \(BD\) и \(DC\) так, что отношение длин этих отрезков равно отношению длин прилежащих сторон \(AB\) и \(AC\). То есть, \(\frac{BD}{DC} = \frac{AB}{AC}\). Подставляя известные значения, получаем \(\frac{BD}{DC} = \frac{20}{5} = 4\). Отсюда следует, что \(BD = 4 \cdot DC\).
Мы знаем, что отрезки \(BD\) и \(DC\) составляют всю сторону \(BC\), поэтому \(BD + DC = BC\). Поскольку \(BC = 20\), мы имеем уравнение \(BD + DC = 20\). Заменяя \(BD\) на \(4 \cdot DC\), получаем \(4 \cdot DC + DC = 20\), что упрощается до \(5 \cdot DC = 20\). Делим обе части на \(5\), чтобы найти длину отрезка \(DC\): \(DC = \frac{20}{5} = 4\). Теперь, зная \(DC\), можем найти \(BD\): \(BD = 4 \cdot DC = 4 \cdot 4 = 16\). Проверка: \(BD + DC = 16 + 4 = 20\), что равно длине стороны \(BC\).
Теперь найдем косинус угла \(C\). Поскольку треугольник \(ABC\) равнобедренный с \(AB = BC\), угол \(A\) равен углу \(C\). Для нахождения косинуса угла \(C\) проведем высоту \(BE\) из вершины \(B\) к основанию \(AC\). В равнобедренном треугольнике высота, проведенная к основанию, также является медианой, поэтому точка \(E\) делит основание \(AC\) пополам. Следовательно, \(AE = EC = \frac{AC}{2} = \frac{5}{2} = 2.5\). Треугольник \(BEC\) является прямоугольным с прямым углом при вершине \(E\). В этом прямоугольном треугольнике косинус угла \(C\) определяется как отношение прилежащего катета \(EC\) к гипотенузе \(BC\). Таким образом, \(\cos C = \frac{EC}{BC} = \frac{2.5}{20} = \frac{25/10}{20} = \frac{25}{200} = \frac{1}{8}\).
Теперь у нас есть все необходимые данные для применения теоремы косинусов к треугольнику \(ADC\) с целью нахождения длины биссектрисы \(AD\). По теореме косинусов для стороны \(AD\) в треугольнике \(ADC\): \(AD^2 = AC^2 + CD^2 — 2 \cdot AC \cdot CD \cdot \cos C\). Подставляем известные значения: \(AC = 5\), \(CD = 4\), и \(\cos C = \frac{1}{8}\). Получаем \(AD^2 = 5^2 + 4^2 — 2 \cdot 5 \cdot 4 \cdot \frac{1}{8}\). Вычисляем квадраты: \(AD^2 = 25 + 16 — 2 \cdot 5 \cdot 4 \cdot \frac{1}{8}\). Произведение \(2 \cdot 5 \cdot 4 = 40\), поэтому \(AD^2 = 25 + 16 — 40 \cdot \frac{1}{8}\). Умножаем \(40\) на \(\frac{1}{8}\): \(40 \cdot \frac{1}{8} = \frac{40}{8} = 5\). Таким образом, \(AD^2 = 25 + 16 — 5\). Складываем и вычитаем: \(AD^2 = 41 — 5 = 36\). Чтобы найти длину \(AD\), извлекаем квадратный корень из \(36\): \(AD = \sqrt{36} = 6\).
Длина биссектрисы \(AD\) равна \(6\). Ответ совпадает с примером.
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.