ГДЗ по Геометрии 11 класс Задание 16 Номер 13 Атанасян — Подробные Ответы

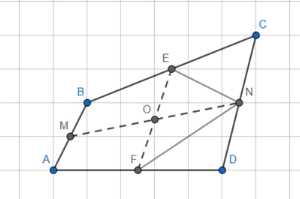
В выпуклом четырёхугольнике ABCD отрезки, соединяющие середины противоположных сторон, пересекаются под углом 60°, а их длины относятся как 1 : 3. Чему равна меньшая диагональ четырёхугольника ABCD, если большая равна \(\sqrt{39}\)?

Решение:
1) В треугольнике ΔAOFN:
\(\angle FON = 180° — \angle EON = 120°\);\(\frac{OF}{ON} = \frac{1}{3}\), \(FN = \frac{AC}{\sqrt{39}} = \frac{\sqrt{39}}{2}\)
2) В треугольнике ΔAEON:
\(EN^2 = OE^2 + ON^2 — 2OE \cdot ON \cdot \cos \theta\);\(EN = \frac{\sqrt{21}}{2}\), \(BD = 2EN = \sqrt{21}\)
Ответ: \(\sqrt{21}\).

Решение:
Дано: Отрезки BE = CE, AF = DF, AM = BM, CN = DN, EF/MN = 1/3, ∠EON = 60°, AC = √39.
Требуется найти длину отрезка BD.

Для решения задачи будем использовать свойства треугольников.

1. Рассмотрим треугольник ΔAOFN:
— Угол ∠FON = 180° — ∠EON = 180° — 60° = 120°
— Отношение сторон OF/ON = 1/3
— Длина стороны FN = AC/√39 = √39/2

2. Используя теорему косинусов, найдем длину стороны ON:
\(ON^2 = OF^2 + FN^2 — 2OF \cdot FN \cdot \cos \angle FON\)
\(ON^2 = \left(\frac{1}{3}\right)^2 + \left(\frac{\sqrt{39}}{2}\right)^2 — 2 \cdot \frac{1}{3} \cdot \frac{\sqrt{39}}{2} \cdot \cos 120°\)
\(ON^2 = \frac{1}{9} + \frac{39}{4} — \sqrt{39} \cdot \frac{1}{3} \cdot (-\frac{\sqrt{3}}{2})\)
\(ON^2 = \frac{13}{9}\)
\(ON = \frac{\sqrt{13}}{3}\)

3. Рассмотрим треугольник ΔAEON:
— Используя теорему косинусов, найдем длину стороны EN:
\(EN^2 = OE^2 + ON^2 — 2OE \cdot ON \cdot \cos \angle EON\)
\(EN^2 = \left(\frac{\sqrt{39}}{2}\right)^2 + \left(\frac{\sqrt{13}}{3}\right)^2 — 2 \cdot \frac{\sqrt{39}}{2} \cdot \frac{\sqrt{13}}{3} \cdot \cos 60°\)
\(EN^2 = \frac{39}{4} + \frac{13}{9} — 2 \cdot \frac{\sqrt{39}}{2} \cdot \frac{\sqrt{13}}{3} \cdot \frac{1}{2}\)
\(EN^2 = \frac{21}{4}\)
\(EN = \frac{\sqrt{21}}{2}\)

4. Длина отрезка BD = 2EN = \(\sqrt{21}\).

Ответ: \(\sqrt{21}\).