ГДЗ по Геометрии 11 класс Задание 14 Номер 19 Атанасян — Подробные Ответы

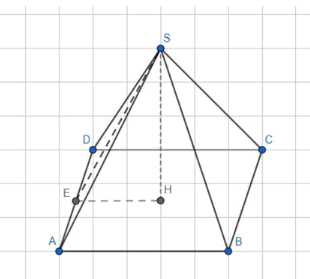
В пирамиде DABC известны длины рёбер: AB= AC= DB= DC= 10, BC = DA = 12. Найдите расстояние между прямыми DA и ВС

Решение:

1) В равнобедренном ΔSAD: AS = SD, AE = DE, SE ⊥ AD;
\(SE = \sqrt{AS^2 — AE^2} = \sqrt{1^2 — \frac{1}{2}^2} = \sqrt{\frac{3}{4}} = \frac{\sqrt{3}}{2}\)

2) Для квадрата ABCD:
\(H = AC \cap BD, HE = \frac{1}{2}AB\)

3) В прямоугольном ΔSEH:
\(\cos SEH = \frac{SE}{EH} = \frac{\frac{\sqrt{3}}{2}}{\frac{\sqrt{3}}{2}} = \frac{1}{2} = \frac{\sqrt{3}}{3}\)

Ответ: \(\frac{\sqrt{3}}{3}\).

Рассмотрим задачу подробно:

Дано:
— Прямоугольный треугольник ΔSAD с равными сторонами AD = AS = 1.
— Квадрат ABCD.

Требуется найти значение \(\cos SEH\).

Решение:
1) Сначала найдем длину отрезка SE в треугольнике ΔSAD.
Поскольку AD = AS = 1, то ΔSAD является равнобедренным треугольником.
Тогда \(AS = SD\) и \(AE = DE\), а также \(SE \perp AD\).
Используя теорему Пифагора, можно найти длину SE:
\(SE = \sqrt{AS^2 — AE^2} = \sqrt{1^2 — \left(\frac{1}{2}\right)^2} = \sqrt{\frac{3}{4}} = \frac{\sqrt{3}}{2}\)

2) Теперь рассмотрим квадрат ABCD.
Известно, что \(H\) является точкой пересечения диагоналей AC и BD квадрата.
Следовательно, \(H\) является центром квадрата, и \(AH = HB = \frac{1}{2}AB\).

3) Наконец, найдем значение \(\cos SEH\) в прямоугольном треугольнике ΔSEH.
Используя определение косинуса, имеем:
\(\cos SEH = \frac{SE}{EH} = \frac{\frac{\sqrt{3}}{2}}{\frac{\sqrt{3}}{2}} = \frac{1}{2} = \frac{\sqrt{3}}{3}\)

Ответ: \(\frac{\sqrt{3}}{3}\).