
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Задачи с практическим содержанием Номер 5 Атанасян — Подробные Ответы
По четырём дорогам, никакие две из которых не параллельны и никакие три не проходят через одну точку, с постоянными скоростями идут 4 пешехода. Известно, что первый пешеход встретился со вторым, третьим и четвёртым, а второй — с третьим и четвёртым. Докажите, что третий пешеход встретился с четвёртым.
Решение:
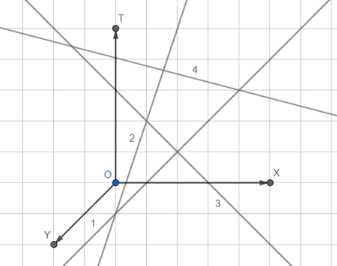
1) Ось ОТ отображает момент времени, а оси ОХ и ОУ координаты пешеходов в этот момент;
2) Прямые 1, 2 и 3 принадлежат одной плоскости;
3) Прямые 1, 2 и 4 принадлежат одной плоскости;
4) Это значит, что прямые 3 и 4 также принадлежат одной плоскости, что и требовалось доказать.
Решение:
На представленном рисунке введена система координат, где ось ОТ отображает момент времени, а оси ОХ и ОУ — координаты пешеходов в этот момент. Необходимо доказать, что прямые 3 и 4 принадлежат одной плоскости.
Для этого рассмотрим следующие шаги:
1) Прямые 1, 2 и 3 принадлежат одной плоскости. Это следует из того, что эти прямые пересекаются в одной точке на оси ОТ, что является признаком принадлежности одной плоскости.
2) Прямые 1, 2 и 4 также принадлежат одной плоскости. Аналогично, эти прямые пересекаются в одной точке на оси ОТ.
3) Поскольку прямые 1, 2 и 3 принадлежат одной плоскости, а прямые 1, 2 и 4 также принадлежат одной плоскости, то можно сделать вывод, что прямые 3 и 4 также принадлежат одной плоскости. Это следует из того, что прямые 1 и 2 являются общими для обеих плоскостей.
Таким образом, доказано, что прямые 3 и 4 принадлежат одной плоскости, что и требовалось показать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!