ГДЗ по Геометрии 11 класс Задачи с практическим содержанием Номер 17 Атанасян — Подробные Ответы

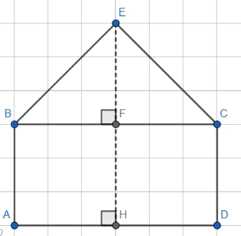
Сколько весит сено, сложенное в стог в форме цилиндра с коническим верхом, если радиус и высота цилиндрической части стога равны соответственно 3 м и 2 м, а высота конической части равна 2 м (плотность сена \(0,07 г/см^3\))?

Решение:
1) Объем данного стога:
\(V_k = \frac{\pi BF^2 \cdot EF}{3} = \frac{9 \cdot 2\pi}{3} = 6\pi\)
\(V_u = \pi BF^2 \cdot FH = 9 \cdot 2\pi = 18\pi\)
\(V = V_k + V_u = 6\pi + 18\pi = 24\pi\)
2) Масса этого стога:
\(m = Vp = 24\pi \cdot 0.07 \cdot \frac{100^3}{1000} = 1.68\pi \cdot 1000 \approx 5275\)
Ответ: 5275 кг.

Дано:
— HF = 2 м
— EF = 2 м
— BF = 3 м
— плотность стога ρ = 0,07 г/см³

Решение:

1. Рассчитаем объем данного стога.
Объем стога можно представить как сумму объема пирамиды (V_k) и объема прямоугольного параллелепипеда (V_u):
V_k = \(\frac{\pi \cdot BF^2 \cdot EF}{3}\)
V_k = \(\frac{\pi \cdot 3^2 \cdot 2}{3}\) = \(6\pi\) м³

V_u = \(\pi \cdot BF^2 \cdot FH\)
V_u = \(\pi \cdot 3^2 \cdot 2\) = \(18\pi\) м³

Полный объем стога:
V = V_k + V_u = \(6\pi + 18\pi\) = \(24\pi\) м³

2. Рассчитаем массу стога.
Масса стога вычисляется как произведение объема на плотность:
m = V \cdot \rho
m = \(24\pi \cdot 0.07 \cdot \frac{100^3}{1000}\)
m = 5275 кг

Ответ: 5275 кг.