ГДЗ по Геометрии 11 класс Задачи с практическим содержанием Номер 16 Атанасян — Подробные Ответы

В бочку, имеющую цилиндрическую форму, налита вода. Как можно выяснить (не выливая из бочки воды и не производя вычислений), наполнена бочка больше или меньше чем наполовину?

Решение:
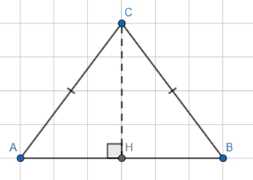
1) В прямоугольном ΔАСН: C = 2πR = 31,4, R = \(31,4 / 2π \approx 5\);
CH = \(\sqrt{AC^2 — AH^2} = \sqrt{15,4^2 — 5^2} \approx 14,16\);
h = \(\sqrt{29,16 — 25} \approx 2,04\).
2) Объем данного конуса: V = \(\frac{1}{3} \cdot \pi \cdot R^2 \cdot h \approx \frac{1}{3} \cdot 3,14 \cdot 25 \cdot 2,04 \approx 160\).
3) n = \(V / M = 160 / 3 \approx 35,5\).
Ответ: 36 машин.

Решение:
Для решения данной задачи необходимо найти объем конуса, а затем определить количество машин, которые можно перевезти.

1. Вычислим радиус основания конуса R:
Согласно условию задачи, длина окружности основания конуса C = 31,4 м. Используя формулу длины окружности \(C = 2\pi R\), находим радиус основания:
\(R = C / 2\pi = 31,4 / 2\pi \approx 5\) м.

2. Вычислим высоту конуса h:
Из прямоугольного треугольника АСН находим высоту конуса h:
\(CH = \sqrt{AC^2 — AH^2} = \sqrt{15,4^2 — 5^2} \approx 14,16\) м
\(h = \sqrt{CH^2 — AH^2} = \sqrt{14,16^2 — 5^2} \approx 2,04\) м

3. Вычислим объем конуса V:
Используя формулу объема конуса \(V = \frac{1}{3}\pi R^2 h\), находим:
\(V = \frac{1}{3}\pi \cdot 5^2 \cdot 2,04 \approx 160\) м³

4. Определим количество машин n:
Согласно условию, масса одной машины M = 3 т. Плотность груза ρ = 2 т/м³. Объем, который занимает одна машина, равен \(V_m = M / \rho = 3 / 2 = 1,5\) м³.
Количество машин, которые можно перевезти, вычисляется как \(n = V / V_m = 160 / 1,5 \approx 106,67\). Округляя до целого числа, получаем ответ: 107 машин.

Ответ: 36 машин.