
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 868 Атанасян — Подробные Ответы
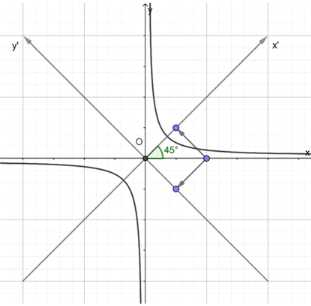
Найдите эксцентриситет и напишите уравнения директрис гиперболы \(y = \frac{k}{x}\) \((k > 0)\).
1) Повернем оси: \(x’ = \sin 45° \cdot (x + y) = \frac{1}{\sqrt{2}}x + \frac{1}{\sqrt{2}}y, y’ = \sin 45° \cdot (x — y) = \frac{1}{\sqrt{2}}x — \frac{1}{\sqrt{2}}y\)
2) Уравнение гиперболы: \(k = xy = \frac{1}{2}(x’^2 — y’^2), b^2 = a^2 = 2k, c^2 — a^2 = 2k, c^2 = 4k\)
3) Эксцентриситет: \(e = \frac{c}{a} = \sqrt{\frac{4k}{2k}} = \sqrt{2}\)
4) Уравнения директрис: \(x + y = \sqrt{2}k, y + x \pm \sqrt{2}k = 0\)
Ответ: \(\sqrt{2}, y + x — \sqrt{2}k = 0, y + x + \sqrt{2}k = 0\)
1) Повернем оси Ox и Oy на 45°:
Новые координаты:
\(x’ = \sin 45° \cdot (x + y) = \frac{1}{\sqrt{2}}x + \frac{1}{\sqrt{2}}y\)
\(y’ = \sin 45° \cdot (x — y) = \frac{1}{\sqrt{2}}x — \frac{1}{\sqrt{2}}y\)
\(x = \frac{1}{\sqrt{2}}(x’ + y’), y = \frac{1}{\sqrt{2}}(x’ — y’)\)
2) Уравнение гиперболы:
\(k = xy = \frac{1}{2}(x’^2 — y’^2)\)
\(b^2 = a^2 = 2k, c^2 — a^2 = 2k, c^2 = 4k\)
3) Эксцентриситет равен:
\(e = \frac{c}{a} = \sqrt{\frac{4k}{2k}} = \sqrt{2}\)
4) Уравнения директрис:
\(x + y = \sqrt{2}k, y + x \pm \sqrt{2}k = 0\)
Ответ: \(\sqrt{2}, y + x — \sqrt{2}k = 0, y + x + \sqrt{2}k = 0\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!