ГДЗ по Геометрии 11 класс Номер 857 Атанасян — Подробные Ответы

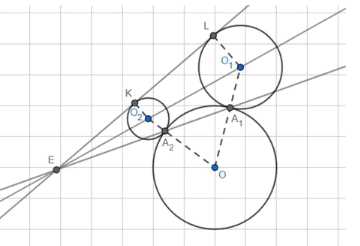
Окружность с центром \(О\) касается двух неравных окружностей с центрами \(O_1\) и \(O_2\) в точках \(А_1\) и \(А_2\) соответственно. Докажите, что прямая \(А_1А_2\) проходит через точку пересечения прямой \(O_1O_2\) и общей касательной (внешней или внутренней) к окружностям с центрами \(O_1\) и \(O_2\)

1) 01А1 = r1; 02А2 = r2; 0А1 = 0А2 = r (так как точка касания окружностей лежит на прямой, соединяющей их центры);
2) Рассмотрим ΔЕКО2 и ΔLЕО1: ∠LЕО1 = ∠КОЕ2 = 90°, значит ΔЕКО2 ~ ΔLЕО1 (по первому признаку), отсюда \(\frac{EО1}{KО2} = \frac{r1}{r2}\);
3) Тогда по теореме Менелая в ΔОА1О2: \(\frac{ОА1}{О1Е} \cdot \frac{О2А2}{ОЕ} \cdot \frac{r}{r1r2} = 1\), значит точки А1, А2 и Е лежат на одной прямой, то есть Е ∈ А1А2, что и требовалось доказать.

Дано: Окружности (0;r); (О1; r1); (О2; r2); 0 ∩ О1 = А1; 0 ∩ О2 = А2; KL — общая касательная к окр О1 и О2; Е = KL ∩ О1О2; Требуется доказать: Е ∈ А1А2.

Доказательство:
1) Рассмотрим треугольник О1А1А2. Так как точка касания окружностей лежит на прямой, соединяющей их центры, то О1А1 = r1, О2А2 = r2, ОА1 = ОА2 = r.

2) Рассмотрим ΔЕКО2 и ΔLЕО1. Так как ∠LЕО1 = ∠КОЕ2 = 90°, то ΔЕКО2 ~ ΔLЕО1 (по первому признаку подобия треугольников). Следовательно, \(\frac{ЕО1}{КО2} = \frac{r1}{r2}\).

3) Применим теорему Менелая к ΔОА1О2. Имеем: \(\frac{ОА1}{О1Е} \cdot \frac{О2А2}{ОЕ} \cdot \frac{r}{r1r2} = 1\). Это означает, что точки А1, А2 и Е лежат на одной прямой, то есть Е ∈ А1А2, что и требовалось доказать.