
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 856 Атанасян — Подробные Ответы
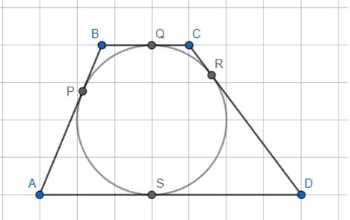
Окружность, вписанная в четырёхугольник \(ABCD\), касается сторон \(AB\), \(ВС\), \(CD\) и \(DA\) соответственно в точках \(P\), \(Q\), \(R\) и \(S\). Докажите, что прямые \(PQ\), \(RS\) и \(АС\) пересекаются в одной точке или параллельны друг другу.
Доказательство: 1) \(BQ = BP, CQ = CR, DR = DS, AS = AP\) (как отрезки касательных, проведенных из одной точки); 2) Таким образом, \(\frac{AP}{PB} = \frac{BQ}{QC} = \frac{CR}{RD} = \frac{DS}{AS} = 1\), следовательно, по доказанному в задаче 855, прямые \(PQ, RS\) и \(AC\) пересекаются в одной точке или параллельны друг другу, что и требовалось доказать.
Дано: четырехугольник ABCD, вписанная окружность O касается сторон AB, BC, CD и AD в точках P, Q, R и S соответственно.
Доказательство:
1) Рассмотрим треугольники BPQ и CQR. Так как точки P, Q, R лежат на окружности, то углы BPQ и CQR вписанные, следовательно, \(BPQ = BCQ\) и \(CQR = BQR\).
2) Аналогично, рассмотрим треугольники DRS и ASD. Так как точки R, S, D лежат на окружности, то углы DRS и ASD вписанные, следовательно, \(DRS = DAS\) и \(ASD = RSD\).
3) Таким образом, \(BPQ = BCQ\), \(CQR = BQR\), \(DRS = DAS\) и \(ASD = RSD\).
4) Из равенства углов следует, что \(BQ = BP\), \(CQ = CR\), \(DR = DS\) и \(AS = AP\).
5) Теперь рассмотрим отношения отрезков: \(\frac{AP}{PB} = \frac{BQ}{QC} = \frac{CR}{RD} = \frac{DS}{AS} = 1\).
6) Согласно теореме 855, прямые PQ, RS и AC либо пересекаются в одной точке, либо параллельны.
Таким образом, доказано, что прямые PQ, RS и AC пересекаются в одной точке или параллельны друг другу.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!