ГДЗ по Геометрии 11 класс Номер 854 Атанасян — Подробные Ответы

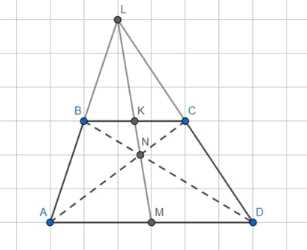
Докажите, что середины оснований трапеции, точка пересечения её диагоналей и точка пересечения продолжений боковых сторон лежат на одной прямой.

1) Так как ΔDAB = ΔCBL и ΔADC = ΔBCL (как соответственные), то ΔABC ~ ΔALD.
2) Проведем медиану LM, так как BC ∥ AD и K — середина BC, то точка K ∈ LM.
3) ΔKNC = ΔANM (как вертикальные) и ΔNMA = ΔNKC (как накрест-лежащие), значит ΔKNC ~ ΔANM.
4) \(\frac{AL}{BL} = \frac{AM}{BK}\) (так как ΔABC ~ ΔALD) и \(\frac{CN}{AN} = \frac{KC}{AM}\) (т.к. ΔKNC ~ ΔANM), отсюда \(\frac{AL}{BL} \cdot \frac{BK}{CK} \cdot \frac{CN}{AN} = \frac{AM}{BK} \cdot \frac{KC}{AM} = 1\).
5) Таким образом, точки L, K, M, N принадлежат одной прямой.

Полное пошаговое решение:

Дано: четырехугольник ABCD является трапецией, точки K и M — середины оснований BC и AD соответственно, точка N — пересечение диагоналей, точка L — пересечение продолжений AB и DC.

Необходимо доказать, что точки L, K, M, N лежат на одной прямой.

Доказательство:
1) Так как ΔDAB = ΔCBL и ΔADC = ΔBCL (как соответственные углы), то ΔABC ~ ΔALD.

2) Проведем медиану LM треугольника ΔALD. Так как BC ∥ AD и K — середина BC, то точка K принадлежит медиане LM, то есть K ∈ LM.

3) Рассмотрим углы ΔKNC и ΔANM. Так как углы KNC и ANM вертикальные, то ΔKNC = ΔANM. Также углы NKC и NAM являются накрест-лежащими, поэтому ΔNKC = ΔNAM. Следовательно, ΔKNC ~ ΔANM.

4) Применим теорему Менелая к треугольникам ΔABC и ΔALD:
\(\frac{AL}{BL} = \frac{AM}{BK}\) (так как ΔABC ~ ΔALD)
\(\frac{CN}{AN} = \frac{KC}{AM}\) (так как ΔKNC ~ ΔANM)
Перемножая эти равенства, получаем:
\(\frac{AL}{BL} \cdot \frac{BK}{CK} \cdot \frac{CN}{AN} = \frac{AM}{BK} \cdot \frac{KC}{AM} = 1\)

5) Таким образом, по теореме Менелая точки L, K, M, N лежат на одной прямой.

Следовательно, доказано, что точки L, K, M, N принадлежат одной прямой.