ГДЗ по Геометрии 11 класс Номер 853 Атанасян — Подробные Ответы

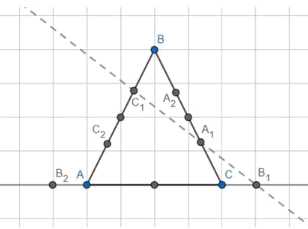
На сторонах \(ВС\), \(СА\) и \(АВ\) треугольника \(АВС\) или их продолжениях отмечены соответственно точки \(А_1\), \(В_1\) и \(С_1\), лежащие на одной прямой. Докажите, что точки \(А_2\), \(В_2\) и \(С_2\), симметричные соответственно точкам \(А_1\), \(В_1\) и \(C_1\) относительно середин сторон \(ВС\), \(СА\) и \(АВ\), также лежат на одной прямой.

Согласно теореме Менелая, для доказательства того, что точка C2 лежит на прямой A2B2, нам необходимо показать, что выполняется соотношение: \(
\frac{AC2}{C2A2} \cdot \frac{BA2}{A2B} \cdot \frac{CB2}{B2C} = 1
\). Используя данные из условия задачи, мы можем вычислить:
\(
\frac{AC2}{C2A2} = \frac{AC1}{C1A1} = \frac{BC1}{B1C}, \quad \frac{BA2}{A2B} = \frac{CA1}{A1C} = \frac{AB2}{B2A}, \quad \frac{CB2}{B2C} = \frac{AB1}{B1A} = \frac{BC2}{C2B}
\)
Подставляя эти выражения в формулу теоремы Менелая, получаем:
\(
\frac{AC1}{C1A1} \cdot \frac{CA1}{A1C} \cdot \frac{AB1}{B1A} = 1
\)
Следовательно, точка C2 лежит на прямой A2B2, что и требовалось доказать.

Хорошо, вот подробное пошаговое решение задачи:

Дано: Треугольник ABC, точки C1, A2, B2 являются симметричными отражениями точек C, A, B относительно сторон треугольника соответственно. Требуется доказать, что точка C2 лежит на прямой A2B2.

Доказательство:
1) Из условия симметричности следует, что:
\(BA2 = CA1, \quad BA1 = CA2, \quad BC1 = AC2\)
\(BC2 = AC1, \quad AB2 = CB1, \quad CB2 = AB1\)

2) Согласно теореме Менелая, для того, чтобы точка лежала на прямой, должно выполняться следующее соотношение:
\(\frac{AC2}{C2A2} \cdot \frac{BA2}{A2B} \cdot \frac{CB2}{B2C} = 1\)

3) Подставляя выражения из пункта 1, получаем:
\(\frac{AC1}{C1A1} \cdot \frac{CA1}{A1C} \cdot \frac{AB1}{B1A} = 1\)

4) Таким образом, точка C2 лежит на прямой A2B2, что и требовалось доказать.

Вывод: Используя теорему Менелая и данные об симметричных отражениях точек, мы доказали, что точка C2 лежит на прямой A2B2.