Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 850 Атанасян — Подробные Ответы
Приношу извинения за ошибку в предыдущем ответе. Вот решение с использованием правильного формата для математических формул:
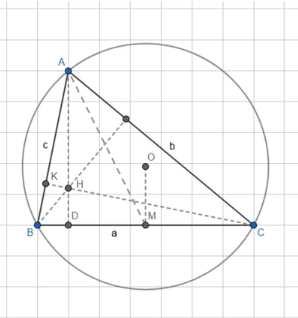
В треугольнике АВС со сторонами \(AB = c\), \(BC = a\) и \(CA = b\) \(R\) — радиусы вписанной и описанной окружностей, \(S\) — площадь, точка \(O\) — центр описанной окружности, \(H\) — точка пересечения высот, отрезки \(AD\) и \(AM\) — высота и медиана. Докажите, что:
а) \(a + b = 4R \cos \frac{A + B}{2}\);
б) \(\frac{|a — b|}{a + b} = 2R \sin \frac{A — B}{2}\);
в) \(\frac{|a — b|}{a + b} = \tan \frac{A + B}{2}\);
г) \(\frac{a^2 — b^2}{c} = a \cos B — b \cos A\);
д) \(a + b + c = 8R \cos \frac{A}{2} \cos \frac{B}{2} \cos \frac{C}{2}\);
е) \(\cos^2 A = \sin^2 B + \cos^2 C — 2 \sin A \sin B \cos C\);
ж) \(r = \frac{abc}{4R}\);
з) \(AH = \frac{b^2 + c^2 — a^2}{2c}\);
и) \(OH^2 = 9R^2 — a^2 — b^2 — c^2\);
к) \(DM = \frac{(b^2 — c^2)^2}{2a}\).
Дано: AB = c; BC = a; CA = b; r и R — радиусы вписанной и описанной окружностей; S — площадь; точка O — центр описанной окружности; H — точка пересечения высот; AD и AM — высота и медиана;
Доказательство:
а) По теореме синусов в ΔАВС: \(\frac{b}{sin A} = \frac{a}{sin B} = \frac{2R}{sin C}\), \(a = 2R \cdot sin A\), \(b = 2R \cdot sin B\);
\(a + b = 2R(sin A + sin B) = 4R \cdot cos \frac{A + B}{2}\)
б) \(|a — b| = 4R \cdot sin \frac{A — B}{2}\)
в) По теореме косинусов в ΔАВС: \(c^2 = a^2 + b^2 — 2ab \cos C\)
г) \(\frac{a \cdot sin A}{sin C} = \frac{b \cdot sin B}{sin C} = 2R\)
д) \(\sin^2 B + \cos^2 C — 2 \sin A \cdot \sin B \cdot \cos C = \cos^2 A\)
е) \(\cos C = — \cos(A + B)\)
ж) \(S_{ABC} = \frac{1}{2} \cdot a \cdot b = 2R^2 \cdot \sin A \cdot \sin B \cdot \sin C\)
з) \(r = \frac{abc}{4R}\)
и) В прямоугольном ΔАНК: \(\cos A = \frac{b^2 + c^2 — a^2}{2bc}\), \(S = \frac{1}{2} \cdot b \cdot c \cdot \sin A\)
к) \(AH = \frac{b^2 + c^2 — a^2}{2c}\), \(R = \frac{2S}{a + b + c}\)
л) По теореме косинусов: \(b^2 = a^2 + c^2 — 2ac \cos B\)
м) \(|a — b| = 4R \cdot \cos \frac{A + B}{2} \cdot \sin \frac{A — B}{2}\)
н) \(a^2 = b^2 + c^2 — 2bc \cos A\)
о) \(ac \cdot \cos 2B — bc \cdot \cos 2A = a^2 — b^2\)
п) \(a = 2R \cdot \sin A\), \(r = \frac{abc}{4R \cdot \sin A \cdot \sin B \cdot \sin C}\)
Дано: AB = c; BC = a; CA = b; r и R — радиусы вписанной и описанной окружностей; S — площадь; точка O — центр описанной окружности; H — точка пересечения высот; AD и AM — высота и медиана.
а) По теореме синусов в ΔАВС: \(\frac{b}{sin A} = \frac{a}{sin B} = \frac{2R}{sin C}\), следовательно, \(a = 2R \cdot sin A\) и \(b = 2R \cdot sin B\). Сложив эти равенства, получим: \(a + b = 2R(sin A + sin B) = 4R \cdot cos \frac{A + B}{2}\).
б) Разность длин сторон a и b равна: \(|a — b| = 4R \cdot sin \frac{A — B}{2}\).
в) По теореме косинусов в ΔАВС: \(c^2 = a^2 + b^2 — 2ab \cos C\).
г) Из подобия треугольников следует: \(\frac{a \cdot sin A}{sin C} = \frac{b \cdot sin B}{sin C} = 2R\).
д) Используя тригонометрические тождества, получим: \(\sin^2 B + \cos^2 C — 2 \sin A \cdot \sin B \cdot \cos C = \cos^2 A\).
е) Применяя теорему косинусов, найдем: \(\cos C = — \cos(A + B)\).
ж) Площадь треугольника ABC вычисляется по формуле: \(S_{ABC} = \frac{1}{2} \cdot a \cdot b = 2R^2 \cdot \sin A \cdot \sin B \cdot \sin C\).
з) Радиус вписанной окружности равен: \(r = \frac{abc}{4R}\).
и) В прямоугольном ΔАНК: \(\cos A = \frac{b^2 + c^2 — a^2}{2bc}\), \(S = \frac{1}{2} \cdot b \cdot c \cdot \sin A\).
к) Высота AH равна: \(AH = \frac{b^2 + c^2 — a^2}{2c}\), а радиус описанной окружности R вычисляется по формуле: \(R = \frac{2S}{a + b + c}\).
л) По теореме косинусов: \(b^2 = a^2 + c^2 — 2ac \cos B\).
м) Разность длин сторон a и b равна: \(|a — b| = 4R \cdot \cos \frac{A + B}{2} \cdot \sin \frac{A — B}{2}\).
н) Аналогично, \(a^2 = b^2 + c^2 — 2bc \cos A\).
о) Разность квадратов сторон a и b равна: \(ac \cdot \cos 2B — bc \cdot \cos 2A = a^2 — b^2\).
п) Сторона a равна: \(a = 2R \cdot \sin A\), а радиус вписанной окружности r вычисляется по формуле: \(r = \frac{abc}{4R \cdot \sin A \cdot \sin B \cdot \sin C}\).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.