ГДЗ по Геометрии 11 класс Номер 849 Атанасян — Подробные Ответы

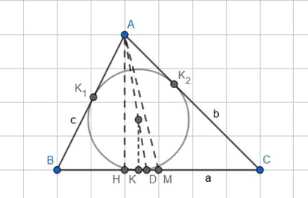
Отрезки AD, AH и AM — биссектриса, высота и медиана треугольника АВС, вписанная в треугольник окружность касается стороны ВС в точке К. Докажите, что \(MK^2 = MD \cdot MH\)

Краткое решение:
1) Пусть AB = c, BC = a, CA = b, при этом b > c
2) BK_1 = BK, CK = CK_2 и AK_1 = AK_2 (как касательные из одной точки), тогда BK + CK + AK_1 = \(\frac{a + b + c}{2} = p\), отсюда CK = p — (BK_1 + K_1A) = p — c
3) AM — медиана, значит BM = MC = \(\frac{a + b — c}{2}\)
4) BD = \(\frac{ac}{b + c}\), по свойству биссектрисы, тогда CD = BC — BD = \(\frac{a — ac}{b + c}\)
5) MD = CD — MC = \(\frac{ab — ac}{2(b + c)} = \frac{a(b — c)}{2(b + c)}\)
6) MH = CH — MC = b \cdot \cos C — \(\frac{a}{2}\) = \(\frac{a^2 + b^2 — c^2}{2a}\)
7) Таким образом: \(MH \cdot MD = \frac{a(b — c)^2}{4(b + c)} = MK^2\), что и требовалось доказать.

Итак, рассмотрим полное пошаговое решение данной задачи:

Дано: ΔABC; AD — биссектриса; AH — высота; AM — медиана; вписанная окружность касается BC в точке K.

Требуется доказать: \(MK^2 = MD \cdot MH\).

Доказательство:
1) Пусть AB = c, BC = a, CA = b, при этом b > c.
2) Так как BK, CK являются касательными к окружности, исходящими из одной точки K, то \(BK_1 = BK\), \(CK_2 = CK\) и \(AK_1 = AK_2\). Следовательно, \(BK + CK + AK_1 = \frac{a + b + c}{2} = p\), откуда \(CK = p — (BK_1 + K_1A) = p — c\).
3) Так как AM является медианой, то \(BM = MC = \frac{a + b — c}{2}\).
4) По свойству биссектрисы, \(BD = \frac{ac}{b + c}\), тогда \(CD = BC — BD = \frac{a — ac}{b + c}\).
5) \(MD = CD — MC = \frac{ab — ac}{2(b + c)} = \frac{a(b — c)}{2(b + c)}\).
6) \(MH = CH — MC = b \cdot \cos C — \frac{a}{2} = \frac{a^2 + b^2 — c^2}{2a}\).
7) Таким образом, \(MH \cdot MD = \frac{a(b — c)^2}{4(b + c)} = MK^2\), что и требовалось доказать.

Итак, мы доказали, что \(MK^2 = MD \cdot MH\), используя свойства биссектрисы, медианы и касательных к окружности.