
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 846 Атанасян — Подробные Ответы
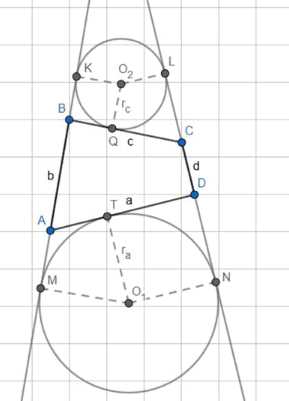
Докажите, что площадь \(S\) выпуклого четырёхугольника со сторонами \(a\), \(b\), \(c\), \(d\) и полупериметром \(p\) выражается формулой \(S = r_a(p — a) + r_c(p — c)\), где \(r_a\) и \(r_c\) — радиусы вневписанных окружностей, касающихся сторон, равных \(a\) и \(c\) (рис. 218).
Дано: ABCD — четырехугольник; АВ = b; BC = c; CD = d; DA = a; р — полуперимтер; вневписанные окружности (О1; ra); (02;rc);
Доказать: SABCD = ra(p — a) +rc(p -c);
Доказательство: Так как АТ, DT, BQ и CL являются касательными, исходящими из одной точки, то АТ = AM, DT = DN, BQ = BK и CL = CQ. Пусть АТ = АМ = k, тогда DT = DN = a — k и BQ = BK = 1, следовательно, CL = CQ = c — l. Так как КМ и LN являются общими касательными к двум окружностям, то \(k + l = \frac{a — b + c + d}{2}\) и KM = \(\frac{a — b + c + d}{2} + b = p\). Так как O1M перпендикулярна МК, а O2K перпендикулярна МК, то O1M || O2K. Аналогично, O1N || O2L, следовательно, O1MKO2 и O1O2LN — прямоугольные трапеции. \(SO1MKO2LN = \frac{1}{2}MK(ra + rc) = \frac{1}{2}p(ra + rc)\). SO1MADN = ra(a) и SBKO2LC = rc(c). Таким образом, SABCD = \(\frac{1}{2}p(ra + rc) — ra(a) — rc(c) = p(ra + rc) — ra(a) — rc(c) = ra(p — a) +\)
\(+ rc(p — c)\), что и требовалось доказать.
Дано: ABCD — четырехугольник; АВ = b; BC = c; CD = d; DA = a; р — полуперимтер; вневписанные окружности (О1; ra); (02;rc);
Доказать: SABCD = ra(p — a) +rc(p -c);
Доказательство:
1) Так как АТ, DT, BQ и CL являются касательными, исходящими из одной точки, то АТ = AM, DT = DN, BQ = BK и CL = CQ.
2) Пусть АТ = АМ = k, тогда DT = DN = a — k и BQ = BK = 1, следовательно, CL = CQ = c — l.
3) Так как КМ и LN являются общими касательными к двум окружностям, то \(k + l = \frac{a — b + c + d}{2}\) и KM = \(\frac{a — b + c + d}{2} + b = p\).
4) Так как O1M перпендикулярна МК, а O2K перпендикулярна МК, то O1M || O2K. Аналогично, O1N || O2L, следовательно, O1MKO2 и O1O2LN — прямоугольные трапеции.
\(SO1MKO2LN = \frac{1}{2}MK(ra + rc) = \frac{1}{2}p(ra + rc)\)
5) SO1MADN = 2SO1AT + 2SO1TD = ra(k + a — k) = ra(a)
SBKO2LC = 2SKBQ + 2SLCQ = rc(1 + c — 1) = rc(c)
6) Таким образом, SABCD = SO1MKO2LN — SO1MADN — SBKO2LC = \(\frac{1}{2}p(ra + rc) — ra(a) — rc(c) = p(ra + rc) — ra(a) — rc(c) = ra(p — a) +\)
\(+ rc(p — c)\), что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!