ГДЗ по Геометрии 11 класс Номер 844 Атанасян — Подробные Ответы

Окружность, касающаяся стороны треугольника и продолжений двух других сторон, называется вневписанной. Докажите, что: а) площадь \(S\) треугольника АВС выражается формулой \(S = r_a(p — a)\), где \(r_a\) — радиус вневписанной окружности, касающейся стороны \(BC = a\), \(p\) — полупериметр треугольника; \(os = \sqrt{r_a r_b r_c}\), где \(r\) — радиус окружности, вписанной в треугольник, \(r_a\), \(r_b\), \(r_c\) — радиусы вневписанных окружностей.

Решение:
1) OL = OM = ON = r; ZLOM = 180° — ZA;
2) \(S_{LOM} = \frac{1}{2} \cdot r \cdot r \cdot \sin \angle LOM = \frac{r^2 \sin \angle A}{AB \cdot AC \sin \angle A} = \frac{r^2}{AB \cdot AC}\)
3) Аналогично находим: \(S_{MON} = \frac{r^2}{CA \cdot CB}, S_{NOL} = \frac{r^2}{BA \cdot BC}\)
4) \(S_{LMN} = S_{LOM} + S_{MON} + S_{NOL} = \frac{r^2(AB + BC + CA)}{AB \cdot BC \cdot CA} \cdot S_{ABC}\)
5) \(S_{ABC} = \frac{AB + BC + CA}{2} \cdot r, \frac{S_{LMN}}{S_{ABC}} = \frac{2r}{AB \cdot BC \cdot CA} \cdot S_{ABC} = \frac{r}{2R}\)

Решение:
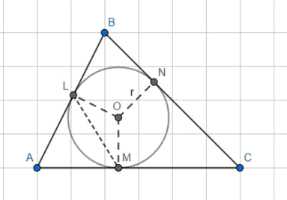
Дано: вписанная окружность касается треугольника ΔABC в точках M, N и L. Известно, что M ∈ AC, N ∈ BC, L ∈ AB.

Требуется доказать, что отношение площади SЛМN к площади SАBC равно отношению радиуса окружности r к 2R, где R — радиус описанной окружности треугольника ΔABC.

Доказательство:
1) Площадь треугольника ΔLOM равна:
\(S_{LOM} = \frac{1}{2} \cdot r \cdot r \cdot \sin \angle LOM\)
Так как ∠LOM = 180° — ∠A, то
\(S_{LOM} = \frac{1}{2} \cdot r^2 \cdot \sin \angle A = \frac{r^2}{AB \cdot AC \sin \angle A} = \frac{r^2}{AB \cdot AC}\)

2) Аналогично находим площади других треугольников:
\(S_{MON} = \frac{r^2}{CA \cdot CB}\)
\(S_{NOL} = \frac{r^2}{BA \cdot BC}\)

3) Площадь SЛМN равна сумме площадей треугольников ΔLOM, ΔMON и ΔNOL:
\(S_{LMN} = S_{LOM} + S_{MON} + S_{NOL} = \frac{r^2(AB + BC + CA)}{AB \cdot BC \cdot CA} \cdot S_{ABC}\)

4) Площадь описанной окружности SАBC равна:
\(S_{ABC} = \frac{AB + BC + CA}{2} \cdot r\)

5) Отношение площадей:
\(\frac{S_{LMN}}{S_{ABC}} = \frac{\frac{r^2(AB + BC + CA)}{AB \cdot BC \cdot CA} \cdot S_{ABC}}{\frac{AB + BC + CA}{2} \cdot r} = \frac{2r}{AB \cdot BC \cdot CA} \cdot S_{ABC} = \frac{r}{2R}\)

Таким образом, доказано, что \(S_{LMN} : S_{ABC} = r : 2R\).