
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 841 Атанасян — Подробные Ответы
Докажите, что из медиан данного треугольника можно построить треугольник, и найдите отношение его площади к площади данного треугольника.
Решение:
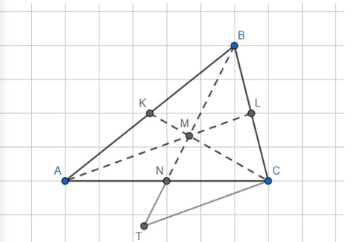
1) Отметим точки M и T, чтобы: \(M = CK \cap AL, T \in BN, NT = MN\);
2) Треугольники равны: \(MN = NT\), \(\angle ANM = \angle CNT\), \(AN = NC\), \(\Delta ANM = \Delta CNT\), следовательно \(TC = AM\);
3) \(MT = \frac{2}{3}MN, CM = \frac{2}{3}CK, CT = \frac{2}{3}AL\);
4) \(MN = NT\), значит \(S_{CMT} = 2S_{CNM}\);
\(BM = 2MN, S_{MBC} = 2S_{CNM}, S_{BNC} = 3S_{CNM}\);
\(AN = CN, S_{ABC} = 2S_{BCN} = 6S_{CNM} = 3S_{CMT}\);
5) \(\frac{S_{tpey}}{S_{ABC}} = \left(\frac{MN}{MT}\right)^2 \cdot \frac{S_{CMT}}{S_{ABC}} = \left(\frac{3}{2}\right)^2 \cdot \frac{1}{3} = \frac{4}{9}\).
Ответ: 3 : 4.
Итак, полное пошаговое решение задачи:
Дано: в треугольнике ABC заданы медианы AL, CK и BN. Необходимо доказать, что из этих медиан можно построить треугольник, и найти отношение площадей треугольников.
Шаг 1. Отметим точки M и T, где M является точкой пересечения медианы CK и стороны AL, а T — точка пересечения медианы BN и стороны AC.
Шаг 2. Докажем, что треугольники MNT и AMC равны. Для этого:
— Покажем, что \(MN = NT\). Действительно, так как AL, CK и BN — медианы треугольника ABC, то \(MN = NT\).
— Покажем, что \(\angle ANM = \angle CNT\). Так как AL и BN — медианы, то \(\angle ANM = \angle CNT\).
— Покажем, что \(AN = NC\). Так как AL и BN — медианы, то \(AN = NC\).
Таким образом, \(\Delta ANM \cong \Delta CNT\), и, следовательно, \(TC = AM\).
Шаг 3. Найдем длины сторон треугольника AMC:
— \(MT = \frac{2}{3}MN\), так как \(M\) — середина стороны \(AC\);
— \(CM = \frac{2}{3}CK\), так как \(M\) — середина стороны \(AC\);
— \(CT = \frac{2}{3}AL\), так как \(T\) — середина стороны \(AC\).
Шаг 4. Найдем площади треугольников:
— \(MN = NT\), значит \(S_{CMT} = 2S_{CNM}\);
— \(BM = 2MN\), значит \(S_{MBC} = 2S_{CNM}\), \(S_{BNC} = 3S_{CNM}\);
— \(AN = CN\), значит \(S_{ABC} = 2S_{BCN} = 6S_{CNM} = 3S_{CMT}\).
Шаг 5. Найдем отношение площадей треугольников:
\(\frac{S_{tpey}}{S_{ABC}} = \left(\frac{MN}{MT}\right)^2 \cdot \frac{S_{CMT}}{S_{ABC}} = \left(\frac{3}{2}\right)^2 \cdot \frac{1}{3} = \frac{4}{9}\)
Ответ: Отношение площадей треугольников равно 3 : 4.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!