
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 840 Атанасян — Подробные Ответы
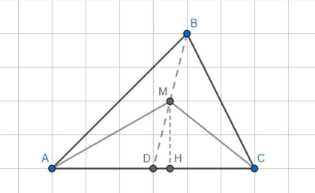
Внутри треугольника АВС взята точка М. Докажите, что площади треугольников ВАМ и ВСМ равны тогда и только тогда, когда точка М лежит на медиане треугольника АВС, проведённой из вершины В
Краткое решение:
1) Пусть BD — медиана, тогда:
\(S_{\text{ABD}} = \frac{1}{2} \cdot \text{AD} \cdot h = \frac{1}{2} \cdot \text{DC} \cdot h = S_{\text{BDC}}\)
2) Опустим перпендикуляр МН на АС:
\(S_{\text{AMD}} = \frac{1}{2} \cdot \text{AD} \cdot \text{MH} = \frac{1}{2} \cdot \text{DC} \cdot \text{MH} = S_{\text{CMD}}\)
\(S_{\text{AMB}} = S_{\text{ADB}} — S_{\text{AMD}} = S_{\text{BDC}} — S_{\text{CMD}} = S_{\text{BMC}}\)
Обратное утверждение:
1) Пусть \(S_{\text{AMB}} = S_{\text{BMC}}\), тогда:
\(S_{\text{AMB}} = \frac{1}{2} \cdot \text{AB} \cdot \text{BM} \cdot \sin \angle \text{ABD}\)
\(S_{\text{BMC}} = \frac{1}{2} \cdot \text{CB} \cdot \text{BM} \cdot \sin \angle \text{CBD}\)
\(\text{AB} \cdot \sin \angle \text{ABD} = \text{CB} \cdot \sin \angle \text{CBD}\)
2) Для треугольников \(\Delta \text{ABD}\) и \(\Delta \text{CBD}\):
\(\frac{1}{2} \cdot \text{BD} \cdot \text{AB} \cdot \sin \angle \text{ABD} = \frac{1}{2} \cdot \text{BD} \cdot \text{CB} \cdot \sin \angle \text{CBD}\)
\(S_{\text{ABD}} = S_{\text{CBD}}, \text{BD} — \text{медиана в } \Delta \text{ABC}\)
Что и требовалось доказать.
Полное пошаговое решение:
Дано: Треугольник ABC, в котором точка M принадлежит стороне AC, а точка D — точка пересечения медианы BM и стороны AC.
Доказать: Если BD является медианой в треугольнике ABC, то площадь треугольника AMB равна площади треугольника BMC.
Решение:
1) Пусть BD является медианой в треугольнике ABC. Тогда, согласно свойствам медианы, мы можем записать:
\(S_{\text{ABD}} = \frac{1}{2} \cdot \text{AD} \cdot h = \frac{1}{2} \cdot \text{DC} \cdot h = S_{\text{BDC}}\)
Где \(h\) — высота треугольника, проведенная из вершины B.
2) Опустим перпендикуляр MH на сторону AC. Тогда:
\(S_{\text{AMD}} = \frac{1}{2} \cdot \text{AD} \cdot \text{MH} = \frac{1}{2} \cdot \text{DC} \cdot \text{MH} = S_{\text{CMD}}\)
\(S_{\text{AMB}} = S_{\text{ADB}} — S_{\text{AMD}} = S_{\text{BDC}} — S_{\text{CMD}} = S_{\text{BMC}}\)
Таким образом, мы доказали, что если BD является медианой в треугольнике ABC, то площадь треугольника AMB равна площади треугольника BMC.
3) Обратное утверждение:
Пусть \(S_{\text{AMB}} = S_{\text{BMC}}\). Тогда:
\(S_{\text{AMB}} = \frac{1}{2} \cdot \text{AB} \cdot \text{BM} \cdot \sin \angle \text{ABD}\)
\(S_{\text{BMC}} = \frac{1}{2} \cdot \text{CB} \cdot \text{BM} \cdot \sin \angle \text{CBD}\)
\(\text{AB} \cdot \sin \angle \text{ABD} = \text{CB} \cdot \sin \angle \text{CBD}\)
4) Для треугольников \(\Delta \text{ABD}\) и \(\Delta \text{CBD}\):
\(\frac{1}{2} \cdot \text{BD} \cdot \text{AB} \cdot \sin \angle \text{ABD} = \frac{1}{2} \cdot \text{BD} \cdot \text{CB} \cdot \sin \angle \text{CBD}\)
\(S_{\text{ABD}} = S_{\text{CBD}}, \text{BD} — \text{медиана в } \Delta \text{ABC}\)
Таким образом, мы доказали, что если площади треугольников AMB и BMC равны, то BD является медианой в треугольнике ABC.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!