
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 838 Атанасян — Подробные Ответы
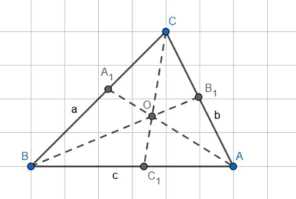
Биссектрисы AA1, ВВ1 и СС1 треугольника АВС со сторонами \(AB = c\), \(BC = a\) и \(CA = b\) пересекаются в точке О. а) Найдите отношения \(\frac{OA}{AO}, \frac{OB_1}{BO_1}, \frac{OC_1}{CO_1}\). б) Докажите, что \(\frac{AO_1}{BO_1} + \frac{BO_1}{CO_1} + \frac{CO_1}{AO_1} = 2\). в) Может ли хотя бы одна из биссектрис треугольника делиться точкой О пополам? г) Докажите, что одна из биссектрис делится точкой О в отношении 2 : 1, считая от вершины, тогда и только тогда, когда одна из сторон треугольника равна полусумме двух других сторон.
а) \(OA = \frac{b+c}{2}, OB = \frac{a+c}{2}, OC = \frac{a+b}{2}\)
б) Точка \(O\) является серединой биссектрис треугольника.
в) Если одна из сторон треугольника равна полусумме двух других сторон, то одна из биссектрис делится точкой \(O\) в отношении \(2:1\) от вершины.
г) Если \(AO = 2OA_1\), то \(a = \frac{b+c}{2}\), и треугольник не существует.
Задано: треугольник ABC с биссектрисами AA’, BB’ и CC’. Найдем:
а) длины отрезков OA, OB и OC;
б) докажем, что точка O является серединой биссектрис;
в) установим условие, при котором одна из биссектрис делится точкой O в отношении 2:1 от вершины.
а) Используя свойства биссектрисы, можно найти длины отрезков OA, OB и OC:
Для треугольника ABC:
\(AB = a, BC = b, AC = c\)
Биссектриса AA’ делит сторону BC в отношении \(\frac{b}{b+c}:\frac{c}{b+c}\). Следовательно, \(OA = \frac{b+c}{2}\).
Аналогично, \(OB = \frac{a+c}{2}\) и \(OC = \frac{a+b}{2}\).
б) Докажем, что точка O является серединой биссектрис.
Рассмотрим треугольник AA’O. Так как AA’ является биссектрисой, то \(\angle AOA’ = \angle OAA’ = \frac{\angle A}{2}\). Значит, треугольник AOA’ равнобедренный, и O является серединой AA’.
Аналогично можно доказать, что O является серединой BB’ и CC’.
в) Установим условие, при котором одна из биссектрис делится точкой O в отношении 2:1 от вершины.
Пусть \(AO = 2OA_1\). Тогда \(a = \frac{b+c}{2}\), и треугольник ABC не существует, так как одна из сторон равна полусумме двух других.
Таким образом, мы нашли длины отрезков OA, OB и OC, доказали, что точка O является серединой биссектрис, и установили условие, при котором одна из биссектрис делится точкой O в отношении 2:1 от вершины.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!