
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 832 Атанасян — Подробные Ответы
Докажите, что в выпуклый многоугольник можно вписать окружность тогда и только тогда, когда окружности, вписанные в два треугольника, на которые он разделяется диагональю, касаются этой диагонали в одной точке.
Краткое решение:
1) Построим перпендикуляры к сторонам: \(O_1 \perp AB\), \(O_1 \perp CB\), \(O_2 \perp DA\), \(O_2 \perp DC\).
2) Пусть \(O_1\) и \(O_2\) касаются АС в точке Е.
3) Касательные из одной точки: \(BP = BK\), \(CP = CE = CN\), \(DM = DN\), \(AK = AE = AM\).
4) В четырехугольнике ABCD: \(AB + CD = AK + KB + CN + ND = AM + BP + CP + DM = AD +\)
\(+ BC\). Значит, можно вписать окружность.
Обратное утверждение:
1) Если в ABCD можно вписать окружность, то \(O_1\) касается АС в точке \(E_1\), \(O_2\) касается АС в точке \(E_2\).
2) В описанном четырехугольнике: \(AB + CD = AD + BC\), \(BP = BK\), \(MD = ND\), \(BP + PC + AM + MD = BK + KA + CN + ND\), \((PC — CN) + (AM — KA) = 0\), \(PC = CN\).
3) Касательные из одной точки: \(PC = CN\), \(CE_1 = PC\), \(CE_2 = CN\), \(CE_1 = CE_2\).
Полное пошаговое решение:
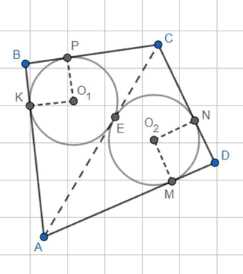
Дано: Окружности \(O_1\) и \(O_2\) вписаны в треугольники АВС и ADC соответственно. Требуется доказать, что в четырехугольнике ABCD можно вписать окружность, если и только если окружности \(O_1\) и \(O_2\) касаются диагонали АС в одной точке.
Доказательство:
1) Построим перпендикуляры к сторонам треугольников: \(O_1 \perp AB\), \(O_1 \perp CB\), \(O_2 \perp DA\), \(O_2 \perp DC\). Эти перпендикуляры пересекают стороны треугольников в точках \(K\), \(P\), \(M\) и \(N\) соответственно.
2) Предположим, что окружности \(O_1\) и \(O_2\) касаются диагонали АС в точке \(E\).
3) Рассмотрим касательные, проведенные из точки \(E\) к окружностям \(O_1\) и \(O_2\). Согласно свойствам касательных, получаем: \(BP = BK\), \(CP = CE = CN\), \(DM = DN\), \(AK = AE = AM\).
4) Теперь рассмотрим четырехугольник ABCD. Сложив длины противоположных сторон, получаем: \(AB + CD = AK + KB + CN + ND = AM + BP + CP + DM = AD +\)
\(+ BC\). Это означает, что в четырехугольнике ABCD можно вписать окружность.
Обратное утверждение:
1) Предположим, что в четырехугольнике ABCD можно вписать окружность. Тогда окружность \(O_1\) касается стороны АС в точке \(E_1\), а окружность \(O_2\) касается стороны АС в точке \(E_2\).
2) Рассмотрим описанный четырехугольник ABCD. Имеем: \(AB + CD = AD + BC\), \(BP = BK\), \(MD = ND\), \(BP + PC + AM + MD = BK + KA + CN + ND\), \((PC — CN) + (AM — KA) = 0\), \(PC = CN\).
3) Касательные, проведенные из точки \(E_1\) к окружности \(O_1\) и из точки \(E_2\) к окружности \(O_2\), совпадают: \(PC = CN\), \(CE_1 = PC\), \(CE_2 = CN\), \(CE_1 = CE_2\).
Таким образом, доказано, что в четырехугольнике ABCD можно вписать окружность, если и только если окружности \(O_1\) и \(O_2\) касаются диагонали АС в одной точке.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!