Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 831 Атанасян — Подробные Ответы
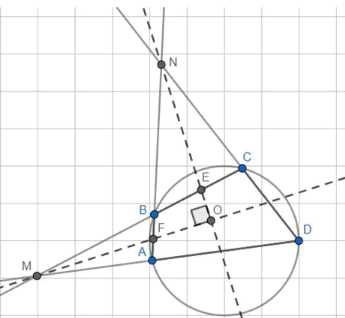
Противоположные стороны выпуклого четырёхугольника продолжены до пересечения. Докажите, что около четырёхугольника можно описать окружность тогда и только тогда, когда биссектрисы образовавшихся углов взаимно перпендикулярны.
Решение:
1) Отметим точки E = NO ∩ BC и F = МО ∩ BA.
2) Пусть прямые МО ∥ NO и обозначим углы: ∠CMO = ∠OMD = a, ∠ANO = ∠OND = φ.
3) В прямоугольном △МЕО и △АNЕ: ∠MEO = 90°, а, ∠NЕС = ∠МЕО; ∠NCЕ = 180°-φ-(90°-a) = 90°+a-φ; ∠BCD = 180°-(90°+a-φ) = 90°-a+φ.
4) В прямоугольном △АNF и △АМF: ∠INF = 90°-φ, ∠MFA = ∠NF; ∠MAF = 180°-a-(90°-φ) = 90°-a+φ; ∠BAD = 180°-(90°-a+φ) = 90°+a-φ.
5) Таким образом, в четырехугольнике ABCD: ∠BAD + ∠BCD = 90°+a-φ+90-a+φ = 180°, значит около него можно описать окружность.
Полное пошаговое решение:
Дано: четырехугольник ABCD, AB ∥ DC = N, CB ∥ DA = M, NO и MO — биссектрисы углов ∠AND и ∠DMC.
Требуется доказать, что можно описать окружность около четырехугольника ABCD тогда и только тогда, когда NO ∥ MO.
Доказательство:
1) Обозначим точки пересечения прямых NO и BC как E, а точки пересечения прямых MO и BA как F.
2) Пусть прямые МО и NO параллельны, и обозначим углы: ∠CMO = ∠OMD = a, ∠ANO = ∠OND = φ.
3) Рассмотрим прямоугольные треугольники МЕО и АNЕ:
— В △МЕО, ∠МЕО = 90°, а, ∠NЕС = ∠МЕО;
— ∠NCЕ = 180°-φ-(90°-a) = 90°+a-φ;
— ∠BCD = 180°-(90°+a-φ) = 90°-a+φ.
4) Рассмотрим прямоугольные треугольники АNF и АМF:
— В △АNF, ∠INF = 90°-φ, ∠MFA = ∠NF;
— ∠MAF = 180°-a-(90°-φ) = 90°-a+φ;
— ∠BAD = 180°-(90°-a+φ) = 90°+a-φ.
5) Таким образом, в четырехугольнике ABCD сумма противоположных углов равна 180°: ∠BAD + ∠BCD = (90°+a-φ) + (90°-a+φ) = 180°.
Следовательно, около четырехугольника ABCD можно описать окружность.
Обратное утверждение:
1) Если ABCD — вписанный четырехугольник, то ∠C + ∠A = 180°, ∠BCN + ∠BAM = 180°.
2) Рассмотрим треугольник АМN:
— 180° — ∠ABC = 2∠BMN + 2∠MNB;
— ∠MON = 180° — (a + ∠BMN) — (φ + ∠BNM);
— ∠MON = 180° — a — φ — (180° — ∠ABC);
— ∠MON = ∠ABC — a — φ.
3) Внешние углы треугольника:
— Для △АBC: ∠ABC = 2φ + ∠BCN;
— Для △МВА: ∠ABC = 2a + ∠BAM;
— 2∠ABC = 2φ + 2a + 180°;
— ∠ABC = φ + a + 90°.
4) Величина угла между МО и NO: ∠MON = φ+a+90°-φ-a = 90°.
Таким образом, если четырехугольник ABCD вписанный, то NO ∥ MO.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.